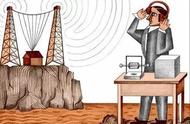
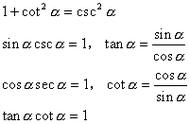然而,科学发现云层的高度不超过,因此我们可以断定,流星不可能是地球上的某种蒸发物,它一定是天外来客!可见,正是正弦定理和余弦定理帮助人类迈出了正确认知这种神秘天文现象的第一步.
3 正、余弦定理与测量问题
正、余弦定理在数学史中与测高、测距等实际问题紧密相关.17世纪以后,随着三角学的发展,人们更多地运用三角学来解决诸多测量问题.特别是到18世纪初,法国数学家马雷(1630—1706)在其著作《实用几何学》中讨论了几类经典的三角学应用问题.

问题Ⅰ:如图,如何测量海岛上某建筑物的高度?
一方面,这个问题的困难之处在于无法测量出观测点到建筑物底部的距离,但是另一方面,借助当时已经发明出来的测角仪,我们可以测量出两个观测点与建筑物底部、建筑物顶部之间产生的各种角度,并且两个陆地观测点之间的距离也是可以知道的.
对此我们可以抽象出如下数学模型:

已知以及角1234以及 CD,求AB.
解答:在中,由正弦定理:

所以