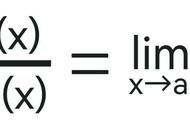如果你读过大学,那么很有可能学过高等数学,对下面几个定理应该有印象吧。
罗尔定理:
如果函数f(x)满足(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)在区间端点处的函数值相等,即f(a)=f(b),那么在(a,b)内至少有一点 ε( a<ε<b),使得f'(ε)=0。
拉格朗日中值定理:
如果函数f(x)满足(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导,那么在(a,b)内至少有一点 ε( a<ε<b),使等式f(b)-f(a)=f'(ε)(b-a)成立。
柯西中值定理:
如果函数f(x)及F(x)满足(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)对任一x∈(a,b),F'(x)≠0,那么在(a,b)内至少有一点 ε( a<ε<b),使等式[f(b)-f(a)]/[F(b)-F(a)]=f'(ε)/F'(ε)成立。
小编整理了一下罗尔定理推导拉格朗日中值定理和柯西中值定理的思路,与大家分享。
罗尔定理推导拉格朗日中值定理的思路:
如果f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,构建一个辅助函数ψ(x)=f(x)-f(a)-[f(b)-f(a)](x-a)/(b-a),显然ψ(x)满足罗尔定理的3个条件,对函数ψ(x)应用罗尔定理,得到结论:在(a,b)内至少有一点ε使得ψ'(ε)=f'(ε)-[f(b)-f(a)]/(b-a)=0成立。即f(b)-f(a)=f'(ε)(b-a)成立。拉格朗日中值定理得证。
罗尔定理推导柯西中值定理的思路:
如果f(x)和F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导;构建一个辅助函数ψ(x)=f(x)-f(a)-[f(b)-f(a)][F(x)-F(a)]/[F(b)-F(a)],显然ψ(x)满足罗尔定理的3个条件,对函数ψ(x)应用罗尔定理,得到结论:在(a,b)内至少有一点ε使得ψ'(ε)=f'(ε)-[f(b)-f(a)]F'(ε)/[F(b)-F(a)]=0成立。因为F'(ε)≠0,所以
[f(b)-f(a)]/[F(b)-F(a)]=f'(ε)/F'(ε)成立。柯西中值定理得证。
以上内容均为个人理解,如有错误,欢迎指正。
,