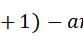今天和大家回顾一下高数当中的微分中值定理,据说是很多高数公式的基础。由于本人才疏学浅,所以对于这点没有太深的认识。但是提出中值定理的几个数学家倒是如雷贯耳,前段时间抽空研究了一下,发现很有意思,完全没有想象中那么枯燥。所以今天的文章和大家聊聊这个话题,我会跳过一些无关紧要或者意义不大的证明部分,尽量讲得浅显有趣一些。
费马引理
首先上场的是费马引理,它是我们介绍后面罗尔中值定理的前提。这个费马引理非常简单,不需要太多篇幅。所以在介绍它之前,先来讲讲费马这个人。
费马在数学届大名鼎鼎,他最著名的理论是费马大小定理。定理的内容我不讲了,和这篇文章也没啥关系。但是这背后有一段著名的故事,说是费马在提出费马大定理的时候并没有觉得它有多么出彩,因此没有加以详细的证明。有一天他在翻阅自己笔记本的时候突然灵感迸发想出了一个绝妙的证明方法。但是由于笔记本旁边空白的区域太小,所以费马这人就在书页边写了一句话,他说:
“
我已发现一种绝妙的证明方法,可惜这里空间太小,写不下。
没想到费马不当回事的定理在日后的数学界非常重要,出人意料的是无数数学家尝试证明费马大定理的正确性,但是都没有成功。虽然这个定理广泛使用,大家也都觉得应该是正确的,但是就是没有人能证明。这一度也称为数学界的顶级难题,一直到1995年,据说也是靠着计算机提供了算力支撑,才终于得以证明。
关于费马在书页边写的绝妙解法,数学界也争论不休。有些人扼腕叹息,觉得是数学界一大损失。还有人觉得这不太靠谱,这可能不是灵感,而是错觉。但无论如何,这也成就了费马,也许他不是史上数学最强的人,但一定是”*“最成功的的一个。
我们来看下来自费马的凝视。

言归正传,我们来看下费马引理。费马引理很简单,是说如果在一段曲线当中存在一个点x0,使得在
x0 的邻域内都存在 f(x) <= f(x0)(或 f(x) >= f(x0)),那么就说明f'(x0)=0。
对导数熟悉的同学会发现,这其实就是把话倒着说。导数为0的点是极值点,既然是极值点显然附近的点要么都大于它或者都小于它。我们看下下图就可以想明白。

证明的过程非常简单,我们令Δx→0 ,那么显然

利用极限左右边界相等,我们就可以证明它的正确性。
罗尔中值定理
罗尔中值定理是在费马引理的基础上做了一点引申,我们还是看上图,在上图当中A和B两点的函数值相等。所以罗尔中值定理是,如果某个函数满足:
- 在闭区间[a, b]上连续
- f(a) = f(b)
- 在开区间(a, b)上可导
那么,在区间(a, b)当中必然存在一个点x0,使得f'(x0) = 0。
这个中值定理也很容易想明白,既然函数在两个端点处值相等,那么无论它是先减再增还是先增再减或者是不增不减,那么显然都会存在至少一个极值点,既然存在极值点,那么根据费马引理显然就有导数为0的点。
拉格朗日中值定理
罗尔定理简单易懂,但是有一个小问题就是限制条件太死,函数上不一定能找到两个点相等。针对这个问题,大佬拉格朗日对这个公式进行了拓展。
他说,只要函数 f(x) 满足:
- 在闭区间[a, b]连续
- 在开区间(a, b)可导
那么就可以找到一个点ξ使得: