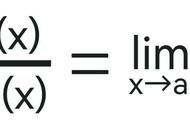拉格朗日中值定理(Lagrange Mean Value Theorem,提出时间1797年)又称拉氏定理,又称微分中值定理,是微分学中的基本定理之一。
它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。
拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形,是泰勒公式的弱形式(一阶展开)。
拉格朗日中值定理是微分中值定理的核心,其他中值定理是拉格朗日中值定理的特殊情况和推广,它是微分学应用的桥梁,在理论和实际中具有极高的研究价值。
一、拉格朗日中值定理的概念和几何意义

2、几何意义:
在满足定理条件的曲线上y=f(x)至少存在一点C1(ξ1,f(ξ1)),该曲线在该点处的切线平行于曲线两端的连线AB(如图)

二、拉格朗日中值定理的应用
1、为什么要用拉格朗日中值定理去解决高考数学问题?
近年来,以高等数学为背景的高考命题成为热点。也就是说,在当前的高考数学试题中,有一些省份或者有一些试题,里面含有了高等数学(大学数学)的成分。这些题目虽然可以利用中学的数学知识解决,但是往往比较繁琐,同时还容易出现证明不下去的尴尬局面。
在这个时候,如果我们提前知道了一些高等数学(大学数学)的相关知识,那么在解题的过程中,相对来说,就简单很多。因为这些高考试题本身就带有高等数学的相关“影子”,同时高等数学的一些知识点,应用到高考题目中,一般只应用一些比较简单的部分,所以此时用高等数学的知识去解决高考压轴大题,就变得简单了。
2、拉格朗日定理具体用来解决哪些类型的数学题目?
一般来说,用来解决高考试题中的函数题、导数题和不等式证明题、恒成立问题、参数范围题等。
三、和拉格朗日定理有关的题目案例分析
【1】直接应用拉格朗日中值定理来解题