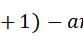函数与其导数是两个不同的函数;而导数只是反映函数在一点的局部特征;如果要了解函数在其定义域上的整体性态,就需要在导数及函数间建立起联系,微分中值定理就是这种作用.微分中值定理,包括罗尔定理、拉格朗日定理、柯西定理、泰勒定理.是沟通导数值与函数值之间的桥梁,是利用导数的局部性质推断函数的整体性质的工具.以罗尔定理、

拉格朗日
中值定理和柯西中值定理组成的一组中值定理是一整个微分学的理论基础.

米歇尔·罗尔
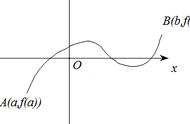
①拉格朗日中值定理:如果函数 满足在闭区间[a,b]上连续;在开区间(a,b)内可导,那么在(a,b)内至少有一点x0 ,使等式f(b)-f(a)=f'(x0)(b-a)成立.
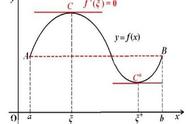
②罗尔定理如果函数 满足在闭区间[a,b]上连续,在开区间(a,b)内可导,在区间端点处的函数值相等,即f(a)=f(b),那么在(a,b)内至少有一点x0 ,使 f'(x0)=0.
中值定理是反映函数与导数之间联系的重要定理,也是微积分学的理论基础,在许多方面它都有重要的作用,在进行一些公式推导与定理证明中都有很多应用。中值定理是由众多定理共同构建的,其中拉格朗日中值定理是核心,罗尔定理是其特殊情况,柯西定理是其推广。

柯西(Cauchy)
微积分是与实际应用联系着发展起来的,它在天文学、力学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学等多个分支中,有越来越广泛的应用。特别是计算机的发明更有助于这些应用的不断发展。客观世界的一切事物,小至粒子,大至宇宙,始终都在运动和变化着。因此在数学中引入了变量的概念后,就有可能把运动现象用数学来加以描述了。
由于函数概念的产生和运用的加深,也由于科学技术发展的需要,一门新的数学分支就继解析几何之后产生了,这就是微积分学。微积分学这门学科在数学发展中的地位是十分重要的,可以说它是继欧氏几何后,全部数学中的最大的一个创造。
因此高考中以中值定理作为基本命题背景,是高考压轴题中非常重要且常见的题型。