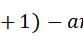中值定理分为:微分中值定理和积分中值定理。
微分中值定理包括罗尔(Rolle)中值定理、拉格朗日(Lagrange)中值定理、柯西(Cauchy)中值定理。其中最重要的内容是拉格朗日定理,可以说其他中值定理都是拉格朗日中值定理的特殊情况或推广。微分中值定理反映了导数的局部性与函数的整体性之间的关系,应用十分广泛。
罗尔中值定理Rolle's theorem提出者:法国人米歇尔·罗尔(Michel Rolle,法,1652-1719)。
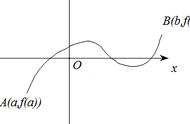
如果 R 上的函数 f(x) 满足以下条件:(1)在闭区间 [a,b] 上连续,(2)在开区间 (a,b) 内可导,(3)f(a)=f(b),则至少存在一个 ξ∈(a,b),使得 f'(ξ)=0。,或者有转折点,导数都是0。

罗尔定理通过下图可以很直观地理解:

假设从时刻a到时刻b,速度v与时间t存在函数关系v(t),如果时间点a与时间点b的速度要相同的话:
情形一:先加速,后降速,则中间一定存在一极值;
情形二:先降速,后加速,则中间一定存在一极值;
情形三:加速、降速、加速、降速,存在三个转折点,三个极值;
情形四:匀速;
实例:用罗尔中值定理证明:方程3ax² 2bx-(a b)=0在 (0,1) 内有实根。
设F(x)=ax³ bx²-(a b)x
则 F(x) 在 [0,1] 上连续,在 (0,1) 内可导,F(0)=F(1)=0,所以由罗尔中值定理,至少存在一点ξ∈(0,1),使得F'(ξ)=0,F'(x)=3ax² 2bx-(a b),所以3aξ² 2bξ-(a b)=0,所以ξ是方程3ax² 2bx-(a b)=0在 (0,1) 内的一个实根。
拉格朗日中值定理Lagrange Mean Value Theorem拉格朗日中值定理又称拉氏定理,是微分学中的基本定理之一,它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形,是泰勒公式的弱形式(一阶展开)。
法国数学家拉格朗日于1797年在其著作《解析函数论》的第六章提出了该定理,并进行了初步证明,因此人们将该定理命名为拉格朗日中值定理。
如果函数f(x)满足:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;
那么在开区间(a,b)内至少有一点ε(a<ε<b)使等式f(b)-f(a)=f'(ε)(b-a)成立。

f'(ε)=(f(b)-f(a))/(b-a)表示函数在闭区间[a,b]上整体变化的平均变化率,f'(ε)表示开区间(a,b)内某点ε处函数的局部变化率。于是,拉格朗日中值公式反映了可导函数在[a,b]上的整体平均变化率与在(a,b)内某点ε处函数的局部变化率的关系。若从力学角度来看,上述中值定理表示整体上的平均速度等于某一内点处的瞬时速度。因此,拉格朗日中值定理是联结局部与整体的纽带。
想像你开始一段跑步,在时间点a、b间,你的速度是f(t),则平均速度就是f'(ε)=(f(b)-f(a))/(b-a)。在整个跑步过程中,你一定会有一个或多个时间点的瞬时速度等于平均速度。
其他形式
记ε=a θ(b-a)(0<θ<1),令a=x, b=x Δx,则有Δy = f(x Δx)-f(x) = f'(x θΔx)Δx(0<θ<1)
上式称为有限增量公式。
在学习微分的时候,我们知道函数的微分dy=f'(x)Δx是函数的增量Δy的近似表达式,一般情况下只有当|Δx|很小的时候,dy和Δy之间的近似度才会提高;而有限增量公式却给出了当自变量x取得有限增量Δx(|Δx|不一定很小)时,函数增量Δy的准确表达式,这就是该公式的价值所在。