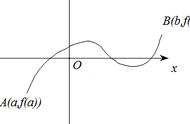
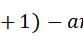积分中值定理在应用中所起到的重要作用是可以使积分号去掉,或者使复杂的被积函数化为相对简单的被积函数,从而使问题简化。因此,对于证明有关题设中含有某个函数积分的等式或不等式,或者要证的结论中含有定积分,或者所求的极限式中含有定积分时,一般应考虑使用积分中值定理, 去掉积分号,或者化简被积函数。
附:
| f(x) | f'(x) | Δx | Δy = f(x Δx)-f(x) | |||||||
| x² | f(b)-f(a) | 2x | dx | = f'(x θΔx)Δx | ||||||
| a | b | a² | b² | b²-a² | 2a | 2b | b-a | θ | θΔx | (0<θ<1) |
| 3 | 4 | 9 | 16 | 7 | 6 | 8 | 1 | 0.5 | 0.5 | 7 |
| 4 | 6 | 16 | 36 | 20 | 8 | 12 | 2 | 0.5 | 1 | 20 |
| 10 | 11 | 100 | 121 | 21 | 20 | 22 | 1 | 0.5 | 0.5 | 21 |
| 11 | 13 | 121 | 169 | 48 | 22 | 26 | 2 | 0.5 | 1 | 48 |
| f(x) | f'(x) | Δx | ||||||||
| b³ | f(b)-f(a) | 3x² | dx | 3a² | ||||||
| a | b | a³ | b³ | b³-a³ | 3a² | 3b² | b-a | θ | θΔx | f'(x θΔx) |
| 3 | 4 | 27 | 64 | 37 | 27 | 48 | 1 | 0.5 | 0.5 | 36.75 |
| 4 | 6 | 64 | 216 | 152 | 48 | 108 | 2 | 0.5 | 1 | 150 |
| 10 | 11 | 1000 | 1331 | 331 | 300 | 363 | 1 | 0.5 | 0.5 | 330.75 |
| 11 | 13 | 1331 | 2197 | 866 | 363 | 507 | 2 | 0.5 | 1 | 864 |
-End-