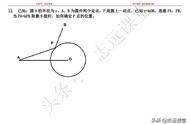
动点问题是中考中非常重要的一类问题,也是中考中的热点问题。动点问题体现了数学中变化的思想,分类讨论的思想,对学生综合运用知识的能力要求非常高。
四边形中的动点问题是一类非常重要的问题,它将三角形和平行四边形、矩形、菱形、正方形结合在一起进行考察。
一、解题基本思路解决动点问题的思路,要注意以下几点:
1、设出未知数
动点问题一般都是求点的运动时间,通常设运动时间为t
2、动点的运动路径就是线段长度
题目通常会给动点的运动速度例如每秒两个单位,那么运动路程就是2t个单位。而2t也就是这个点所运动的线段长。进而能表示其他相关线段的长度。
所以我们在做动点问题的时候,第一步就是把图形中的线段都用含t的代数式来表示。
3、 方程思想求出时间
动点问题通常都是用方程来解决,根据题目找到线段之间的等量关系,然后用含有t的代数式表示出来,列出方程求解出t的值。
4、难点是找等量关系
这种题的难点是找到等量关系。这个等量关系往往不是题目中用语言叙述出来的,而是同学们根据题型自己挖掘出来的等量关系,所以对同学们图形分解的能力以及灵活运用知识的能力要求非常高。
5、注意分类讨论
因为点的运动的位置不同,形成的图形就不同,符合结论的情况可能就不止一种,所以做动点问题要注意分类讨论。
二、实战演练- 1、平行四边形的动点问题

【分析】(1)根据题意可以求得BG=DG,又因为AD与BC平行,所以两直线平行内错角相等得到两对角相等,利用角角边即可得到结论;
(2)第二问要分类讨论,有两种情况。一种情况是F在C的左侧时;第二种情况是点F在C的右侧时去分析,由当图形是平行四边形式AE=CF做等量关系式方程,解方程即可求得答案.

【反思与小结】本题的第二问就用到了分类讨论的思想,因为动点 F与定点c的位置不同,出现两种情况。另外,方程的等量关系是考虑平行四边形的特征得到的。
- 2、菱形的动点问题

【分析】(1)能.首先证明四边形AEFD为平行四边形,当AE=AD时,四边形AEFD为菱形,即40﹣4t=2t,解方程即可解决问题;
(2)直角三角形的行成问题要分三种情形讨论,分类讨论的标准是谁为直角。