【分析】此题不是通过运动形成正方形,而是在正方形里运动。因为动点的运动路径是折线,所以出现等腰三角形的情况不唯一,分三种情况,利用勾股定理和等腰三角形的判定解答即可.

【反思与小结】此题考查正方形的性质,难点在于既有点的运动形成的分类讨论,又有等腰三角形形成的分类讨论。关键是利用勾股定理和等腰三角形的判定.

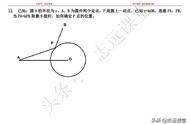
【分析】(1)由于CE平分∠BCA,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF,而OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的角平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.
(2)由(1)得出四边形AECF是矩形,再由平行线得出AC⊥EF,得出四边形AECF是菱形,即可得出结论.