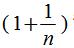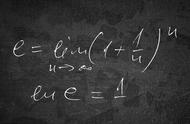1.定义
2.做题手法有界=上界 下界
左极限等于右极限则极限才存在
极限趋于∞:极限不存在
极限趋于0:无穷小
单减数列有下界,必有极限
单增数列有上界,必有极限
收敛必有极限
有极限必收敛
有界不一定有极限
有极限一定有界
(1)等价无穷小替换:

常用等价无穷小替换公式
使用原则:必须为x趋于0时使用;乘除随便用,加减必得分子分母上下同阶才可以使用。
常用套路——三阶无穷小:

三阶无穷小
(2)洛必达法则:
分子分母上下同时求导
使用原则:当分子分母上下同时趋于0(∞);分子分母同时可以求导时方可使用。
(3)泰勒公式:
一般形式:

常见替换:

使用规则:展开到幂数最低
,