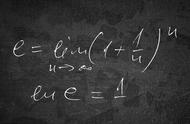以下是小编为考生们梳理的2018考研数学复习:求函数的未定式极限中灵活使用“三尽量”相关内容,希望大家坚守初心,尽全力备战2018考研。
考研数学被大多数考生列为重点逃避对象,究竟考研数学复习过程中,有没有更好的方式方法?选择怎样的参考资料,做哪种类型的练习题才能在短期内提高成绩。很遗憾的告诉大家,基本没有。考研数学是由不同的知识点组合起来,成绩的高低并不仅仅是喜欢数学就能够解决的。勤加练习,熟能生巧,方法公式就摆在课本上,希望考生在日常联系中夯实基础,在考场上才能运用自如。以下是小编为考生们梳理的2018考研数学复习:求函数的未定式极限中灵活使用“三尽量”相关内容,希望大家坚守初心,尽全力备战2018考研。

首先,应尽量通过三角函数、代数的恒等变形,把那些既非无穷大也非无穷小的因子利用极限四则运算分离出去,且尽量利用等价无穷小因子替换以化简分子与分母.若需要利用变量代换化简的,也尽量先用变量代换化简,做完三个“尽量”后,如需要,又满足洛必达法则的条件,才对“干净”的未定式极限使用洛必达法则进行运算. 若是一开始就急于使用洛必达法则,有时会使极限的计算复杂化。
同学们都知道,常见的等价无穷小有:

对于求函数的不定式极限的题目,虽然题目难度不大,用的都是一些基本方法,所以要求同学们对于7种未定式极限的形式会进行转化。此外,要求对于常见的无穷小代换公式一定要熟练掌握。
同学们值得注意的是要正确使用等价无穷小代换的方法。等价无穷小代换可以对分子、分母同时进行,也可以只对分子或分母进行,还可以只对分子或分母中的部分乘积因子进行,但对于分子或分母中的加、减的各项或加、减中的代数和的各项不能分别使用等价无穷小代换. 同学们一定利用好“三尽量”。
大连文都考研会及时为考生们推送各类新鲜、实用且有效的,有关考研数学的复习资料。关注文都考研公众号【dalianwendu2013】,轻按Ctrl D添加收藏,让我们在成长的路上一同前行,2018考研,有你有文都。
大连文都教育(dalianwendu2013)
大连文都君(*18741168185)
,