解决高考数学空间几何二面角的问题,最烧脑的一步就是找到二面角的平面角。那么有没有一种简单粗暴的方法,可以不用找二面角的平面角,直接就把问题解决了呢?那当然是有的了,这就是老黄今天要分享的“建立空间坐标系,利用向量运算的方法”。以下面的这道高考数学空间几何二面角相关的真题为例:
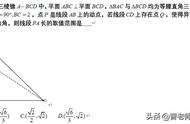
如图, 在四棱锥E-ABCD中, AB//CD, AD=CD=BC=AB/2, E在以AB为直径的半圆(不包括端点),平面ABE⊥平面ABCD,M, N分别为DE,BC的中点.
(1)求证:MN//平面ABE;
(2)当四棱锥E-ABCD体积最大时,求二面角N-AE-B的余弦值.

【第一小题只要注意,BCDE不是一个平面就可以了,否则就很容易出错。注意B,C,D三点在平面ABCD上,没有两个平面存在三个不在同一直线上的公共点的】
(1)证明:过N作NF//AB,交AD于F,
连接MF, 则MF//AE,
∴平面FMN//平面ABE,
∵MN⊂平面FMN, ∴MN//平面ABE.

【第二小题直接建系,不过建系的技巧,以及如何求二面角的平面角的余弦的知识也是要掌握才能做到的。这里要运用“二面角的平面角等于两个平面的法向量之间的夹角”的定理】

(2)解:当点E是弧AB的中点时,四棱锥E-ABCD体积最大,【因为此时四棱柱的高最大,底面积不变】
取AB的中点O为原点建系(如上图),设AD=CD=BC=1,则AB=2,【设AD=a,则解题过程很麻烦,设AD为整体1,则解题过程容易出错,老黄选择后者】
B(0,1,0), A(0,-1,0), E(1,0,0), N(0,3/4,根号3/4),
【下面插入一段求N点坐标的过程:

过C作CF⊥AB于F, 过N作NG⊥AB于G,则BF=OF=CD/2=1/2,
∴GF=BF/2=1/4, FC=根号3BF=根号3/2,
GN=FC/2=根号3/4,OF GF=3/4
所以N(0,3/4,根号3/4),如果你愿意的话,可以把这段写在前面。】
向量AE=(1,1,0), 向量AN=(0,7/4,根号3/4)【求法向量,只需要平面内的两个有交点的向量就够了】
设平面ANE的法向量为n=(x,y,z),
则向量n向量AE=x y=0, 向量n向量AN=7y/4 根号3z/4=0,【因为法向量与平面垂直,所以垂直于平面内的直线,两个向量的积就等于0】
任取x=根号3, 则y=-根号3, z=7,【x可以任取,因为任取法向量上的一点,并不影响后面的运算】
可取平面BAE的法向量m=(0,0,1),【因为平面BAE是水平平面,所以法向量是z轴】
记二面角N-AE-B为α, 则coα=向量m向量 n/(|向量m||向量n|)=7根号55/55. 【求两个向量夹角的余弦,这个公式要牢记】
这个方法,虽然看起来也没有那么简便,但是它胜在直接,不需要过多的思考,没有那么烧脑,掌握并且熟悉了,高中数学中是可以帮大忙的。
,