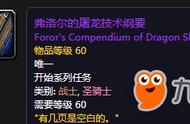
费歇尔小时候有很严重的视力损伤,因此医生禁止他晚上在灯光下阅读。即使后来上学时,他的数学导师也在黑暗中教他数学,黑暗使人强大,长期在黑暗中脑补使得费歇尔形成了强大的几何能力。这也是为什么费歇尔可以很轻易的解决t检验的证明等一系列问题,因为这些问题本质上就是数形结合的问题。费歇尔的黑暗能力使他看到了别人都没有注意到的新概念——自由度。在t检验中,我们首先要计算一个t值,t值的计算方法就是用均值的差值除以标准误(这个我们后面会讲到)。不同自由度下t值的分布是不同的,而一旦给定自由度,t值的分布就固定了(对于很多其他检验也是如此,比如方差分析中的F值),这就是为什么我们在做t检验的时候要在后面的括号里写上自由度,一般情况下,对t检验而言,自由度就是被试量n再减去1。t值的分布不是一个固定的图形,而是一系列图形,费歇尔直接用多维几何把他脑子里在黑暗中呈现的分布族图形给描述出来了,这也是为什么戈赛特和卡尔.皮尔逊看不懂费歇尔的文章。

t值的分布是一个分布族,df就是自由度,对t检验df=n-1,df越大则t值的分布越接近正态分布
上一讲我们说到了集中与平均数,这一讲我们要说变异性了。我们为什么需要变异性?假设你的班主任尝试了新的教学方法,使全班的平均成绩提高了5分,我们能说这个新方法是有效的吗?如果这里的成绩指的是雅思成绩,雅思满分9分,平均提高5分的话这个老师就可以封神了;不过如果这里的成绩指的是SAT,SAT满分1600分,提高5分有可能只是这一次同学们偶然的发挥好了而已。如果不衡量变异性,我们将不知道5分意味着什么。

实验A和实验B中,两组样本的均值差值都是5,但实验A的样本间有明显的不同,两个实验的差别就是变异性的不同
生活中,无论我们测量什么,都有意想不到的变异,我们不能彻底消灭变异,但是却可以测量它。把一组数据中的每一个分数都减去他们的平均数,然后平方(平方是为了消除负号),再把它们加起来,这就是平方和SS(sum of squared deviations)。请记住SS,因为我们之后会经常用上它。

SS有两种计算方法,得到的结果是一样的,右面的方法计算起来容易些,所以叫计算公式
平方和再除以自由度就是方差,对于总体而言,每个数据都是自由的,因此自由度就是总的个数N;对于样本而言,样本均值理论上应该等于总体的均值,用总体均值和前n-1个数据就可以估计最后一个数据,因此只有n-1个数据是自由的,所以样本的自由度是n-1。

由于范围变窄了,样本的变异性要小于总体的变异性,而样本方差除以n-1时弥补了这个差异,就变回“无偏”了
另外,由于平方的操作导致方差的单位不对,如果你测量了几个人的身高(以米作为单位),这组样本的方差的单位将是平方米,因此需要开根号,方差再开根号就是标准差。需要注意的是,我们在第一讲说过,总体和样本的标准差的符号不同。好好理解一下标准差吧,因为下一讲,标准误就要登场了。
,