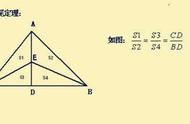
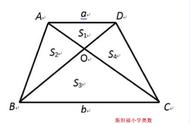
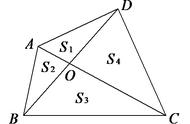
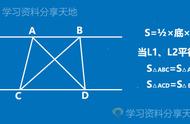
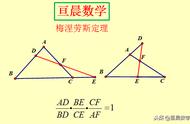
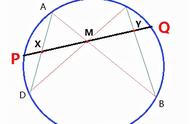
【解题思路】
连接AO,连接BD做辅助线;

设S△BEO的面积为1份;
S△BEO:S△AEO=BE:EA=1:2,故S△AEO的面积为2份;
根据燕尾定理,
S△ABO:S△BDO=AF:FD=1:2,故S△BDO的面积为6份;
S△ADO:S△BDO=AE:EB=2:1,故S△ADO的面积为12份;
S△AFO:S△DFO= AF:FD=1:2,故S△AFO的面积为12÷3=4份,
S△DFO的面积为12÷3×2=8份;
四边形AEOF面积为6份与三角形BDO面积相等,
故平行四边行BODC的面积=12×2=24平方厘米。
下面给学生们留一道练习题,你们可以做一下。
【练习题】
如图,在直角三角形ABC中,已知AC=2厘米,CD=2厘米,CB=3厘米,AM=BM,求三角形ANM的面积?

有关燕尾模型的知识今天就为学生们讲到这里,下次为大家讲解第四大模型——鸟头模型。
大家今后在数学方面有什么问题难题,可以私信向吴老师提问。
,