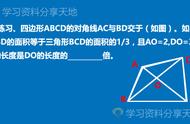
【解答】
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB•AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
同步练习:
1.如图,△ABC与△ADB中,∠ABC=∠ADB=90°,∠C=∠ABD,AC=5cm,AB=4cm,AD的长为()

故答案为:16/5
2.如图,在四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求AC/AF的值.

【解答】
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵AC2=AB•AD,
∴AC/AB=AD/AC,
∴△ADC∽△ACB;
(2)∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
∵点E为AB的中点,
∴CE=AE=½AB=3/2,
∴∠EAC=∠ECA,
∴∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴CE∥AD;
∴CF/FA=CE/AD=3/4,
∴AD/AF=7/4.
温馨提示
希望本文对你有所帮助,请持续关注后续更新的精彩内容!
如您对本文有更多更好的建议,可评论留言,姜姜老师会第一时间回复。

往期精彩:
,