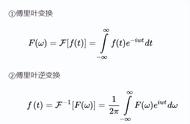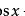1、数学史
数学史是研究数学科学发生发展及其规律的科学,简单地说就是研究数学的历史。它不仅追溯数学内容、思想和方法的演变、发展过程,而且还探索影响这种过程的各种因素,以及历史上数学科学的发展对人类文明所带来的影响。因此,数学史研究对象不仅包括具体的数学内容,而且涉及历史学、哲学、文化学、宗教等社会科学与人文科学内容,是一门交叉性学科。
2、数理逻辑与数学基础
a、演绎逻辑学(亦称符号逻辑学)b、证明论 (亦称元数学) c、递归论 d、模型论 e、公理集合论 f、数学基础 g、数理逻辑与数学基础其他学科
3、数论
数论是纯粹数学的分支之一,主要研究整数的性质。
按研究方法来看,数论大致可分为初等数论和高等数论。初等数论是用初等方法研究的数论,它的研究方法本质上说,就是利用整数环的整除性质,主要包括整除理论、同余理论、连分数理论。高等数论则包括了更为深刻的数学研究工具。它大致包括代数数论、解析数论、计算数论等等。
a、初等数论 b、解析数论 c、代数数论 d、超越数论 e、丢番图逼近 f、数的几何 g、概率数论 h、计算数论 i、数论其他学科
4、代数学
代数学是数学中最重要的、基础的分支之一。代数学的历史悠久,它随着人类生活的提高,生产技术的进步,科学和数学本身的需要而产生和发展。在这个过程中,代数学的研究对象和研究方法发生了重大的变化。代数学可分为初等代数学和抽象代数学两部分。初等代数学是更古老的算术的推广和发展,而抽象代数学则是在初等代数学的基础上产生和发展起来的。初等代数学是指19世纪上半叶以前的方程理论,主要研究某一方程(组)是否可解,怎样求出方程所有的根(包括近似根)以及方程的根所具有的各种性质等。
a、线性代数 b、群论 c、域论 d、李群 e、李代数 f、Kac-Moody代数 g、环论 (包括交换环与交换代数,结合环与结合代数,非结合环与非结 合代数等) h、模论 i、格论 j、泛代数理论 k、范畴论 l、同调代数 m、代数K理论 n、微分代数 o、代数编码理论 p、代数学其他学科
5、代数几何学
代数几何研究就是平面解析几何与三维空间解析几何的推广。大致说来,它是研究n维仿射空间或n维射影空间中多项式方程组的零点集合构成的几何对象之特性及其上的三大结构:代数结构,拓扑结构和序结构。此三大结构是Bourbaki学派(布尔巴基)所提出,用来统摄结构数学,数学中凡是具有结构特征的板块,均由这三大母结构及其混合构成。
6、几何学
a、几何学基础 b、欧氏几何学 c、非欧几何学 (包括黎曼几何学等) d、球面几何学 e、向量和张量分析 f、仿射几何学 g、射影几何学 h、微分几何学 i、分数维几何 j、计算几何学 k、几何学其他学科
7、拓扑学
a、点集拓扑学 b、代数拓扑学 c、同伦论 d、低维拓扑学 e、同调论 f、维数论 g、格上拓扑学 h、纤维丛论 i、几何拓扑学 j、奇点理论 k、微分拓扑学 l、拓扑学其他学科

8、数学分析
又称高级微积分,分析学中最古老、最基本的分支。一般指以微积分学和无穷级数一般理论为主要内容,并包括它们的理论基础(实数、函数和极限的基本理论)的一个较为完整的数学学科。它也是大学数学专业的一门基础课程。数学中的分析分支是专门研究实数与复数及其函数的数学分支。它的发展由微积分开始,并扩展到函数的连续性、可微分及可积分等各种特性。这些特性,有助我们应用在对物理世界的研究,研究及发现自然界的规律。
a、微分学 b、积分学 c、级数论 d、数学分析其他学科
9、非标准分析
非标准分析(Non-standard analysis),数学中利用现代数理逻辑把通常实数结构扩张为包括无穷小与无穷大的结构而形成的一个新分支。
10、函数论
a、实变函数论 b、单复变函数论 c、多复变函数论 d、函数逼近论 e、调和分析 f、复流形 g、特殊函数论 h、函数论其他学科
11、常微分方程
a、定性理论 b、稳定性理论 c、解析理论 d、常微分方程其他学科
12、偏微分方程
a、椭圆型偏微分方程 b、双曲型偏微分方程 c、抛物型偏微分方程 d、非线性偏微分方程 e、偏微分方程其他学科
13、动力系统
a、微分动力系统 b、拓扑动力系统 c、复动力系统 d、动力系统其他学科

14、积分方程
积分方程是含有对未知函数的积分运算的方程,与微分方程相对。许多数学物理问题需通过积分方程或微分方程求解。积分方程是近代数学的一个重要分支。数学、自然科学和工程技术领域中的许多问题都可以归结为积分方程问题。正是因为这种双向联系和深入的特点,积分方程论得到了迅速地发展,成为包括众多研究方向的数学分支。
15、泛函分析
a、线性算子理论 b、变分法 c、拓扑线性空间 d、希尔伯特空间 e、函数空间 f、巴拿赫空间 g、算子代数 h、测度与积分 i、广义函数论 j、非线性泛函分析 k、泛函分析其他学科
16、计算数学
a、插值法与逼近论 b、常微分方程数值解 c、偏微分方程数值解 d、积分方程数值解 e、数值代数 f、连续问题离散化方法 g、随机数值实验 h、误差分析 i、计算数学其他学科
17、概率论
a、几何概率 b、概率分布 c、极限理论 d、随机过程 (包括正态过程与平稳过程、点过程等) e、马尔可夫过程 f、随机分析 g、鞅论 h、应用概率论 (具体应用入有关学科) i、概率论其他学科
18、数理统计学
a、抽样理论 (包括抽样分布、抽样调查等 )b、假设检验 c、非参数统计 d、方差分析 e、相关回归分析 f、统计推断 g、贝叶斯统计 (包括参数估计等) h、试验设计 i、多元分析 j、统计判决理论 k、时间序列分析 l、数理统计学其他学科
19、应用统计数学
a、统计质量控制 b、可靠性数学 c、保险数学 d、统计模拟
20、应用统计数学其他学科
应用统计数学专业是培养具备统计数学和应用数学的基础理论,具有运用数学理论和工具进行实际问题的抽象、分析、解决的能力和较强的计算机运用能力
21、运筹学
a、线性规划 b、非线性规划 c、动态规划 d、组合最优化 e、参数规划 f、整数规划 g、随机规划 h、排队论 i、对策论 亦称博弈论 j、库存论 k、决策论 l、搜索论 m、图论 n、统筹论 o、最优化 p、运筹学其他学科

22、组合数学
组合数学(Combinatorial mathematics),又称为离散数学。
广义的组合数学就是离散数学,狭义的组合数学是图论、代数结构、数理逻辑等的总称。但这只是不同学者在叫法上的区别。总之,组合数学是一门研究离散对象的科学。随着计算机科学的日益发展,组合数学的重要性也日渐凸显,因为计算机科学的核心内容是使用算法处理离散数据。[1]
狭义的组合数学主要研究满足一定条件的组态(也称组合模型)的存在、计数以及构造等方面的问题。 组合数学的主要内容有组合计数、组合设计、组合矩阵、组合优化(最佳组合)等。
23、模糊数学
模糊数学又称Fuzzy 数学,是研究和处理模糊性现象的一种数学理论和方法。
24:量子数学
量子数学是指基于时间和空间的量子性而建立的数学,用于描述真实的物理世界。
25、应用数学 (具体应用入有关学科)
应用数学,本专业培养掌握数学科学的基本理论与基本方法,具备运用数学知识、使用计算机解决实际问题的能力,受到科学研究的初步训练,能在科技、教育和经济部门从事研究、教学工作或在生产经营及管理部门从事实际应用、开发研究和管理工作的高级专门人才。
26、数学其他学科
,