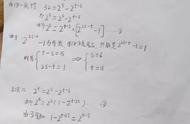(一)。人类数学中最大未解之谜——素数的定理!
素数,指大于1的自然数中,除了1和本身外,不能被其他自然数整除的数,如:2,3,5,7,11……,通常用“p”表示。
素数的分布规律至欧几里德以来就是个迷。今天,我们来认识下,素数的重要分布规律——素数定理。这是目前发现的,最重要的且被证明限制素数分布的定理之一。
欧几里德在大约公元前300年,就漂亮地证明了素数的无限性,从此人们开始了寻找素数公式的历程。

大数学家欧拉在给丹尼尔·伯努利的一封信中写道:"素数的计算公式,在我们这辈子可能找不到了。不过,我还是想用一个式子来表达它,但并不能表示出所有素数。n^2-n 41,n等于1到40"。
欧拉给出的这个多项式,在n=41时失效了,后来哥德巴赫给欧拉的信中提到:"一个整系数多项式,是不可能对所有整数取到素数的,但有些多项式可以得到很多素数。"
后来欧拉漂亮地证明了哥德巴赫的这个猜想,欧拉对数论的贡献相当多,数论四大定理之一就有个——欧拉定理,而欧拉的素数乘积式,是开启黎曼猜想的金钥匙。

欧拉乘积式
对素数的研究,欧拉过后,直到高斯才有了进展,大约在1792年,15岁的高斯就发现,素数在自然数中的分布密度,趋近于类似于对数积分的函数。
同时期的数学家勒让德(A.M.Legendre)也提出了等价的猜想,但他们都无法对其证明,至此,这个问题成了数学界的顶级难题,甚至在数学界流传着:如果谁证明了这个猜想,那么他将会得到永生。

证我者,得永生!
直到一百多后的1896年,这个猜想才被两位年轻的数学家阿达马和德·拉·瓦莱布桑独立证明,他们的证明都是根据黎曼的思路走的,其中运用到了高深的整函数理论,至此,这个猜想正式升级为定理——素数定理(PNT)。

素数定理
值得一提的,他们两人一个活了96岁,一个活了98岁。
素数定理还有个初等表达式:
素数定理初等表达式
该定理可以推出很多有趣的结论,比如:
N是素数的概率~1/lnN;
第N个素数~NlnN; 这个素数定理所要表达的中心意思为:,当自然整数很大时,用这个素数定理求得的数量越来越接近于在自然整数中所存有的实际素数的含有量。
这两个推论和PNT互为充要条件。
虽然我们有了PNT,但是PNT给出的绝对误差实在是糟糕透了,比如第10000个素数104729,而PNT给出的是92103,这是数学家不能接受的,我们想要的是准确的素数公式。
直到黎曼在1859年才给出了π(x)的准确表达式:
黎曼关于素数计数函数π(x)的表达式
但是该表达式基于一个猜想为前提,即大名鼎鼎的黎曼猜想,至今乃是数学界待解决的重要猜想。
(二)。它会无情的走向它的反面。

虽然我们有了PNT,但是PNT给出的绝对误差实在是糟糕透了,比如第10000个素数104729,而PNT给出的是92103,这是数学家不能接受的,我们想要的是准确的素数公式。但仅仅如此吗。 你只要画一个四象线的图形,在这个四象限图形垂直的两条垂直线之外,在第一象限内任意一点处经过0点作一条直线,再向第三象限内延长。
如果把四限限横线等于自然整数中所含有的素数量,把作成的直线等于高斯素数定理所求的含有素数量,那么,当高斯素数定理所求在自然数整数中的素数含有量接近实际含有量相符时,也就是说,接近四像限中的零点时,表明了素数定理的正确性,那么再计算下去呢,根据对顶角相等的性质,得出一个定论,总能误差一样多,如果再计算下去呢,它将失去原有的意义。
,