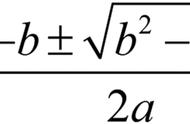1
如何求解一元二次方程 ax² bx c = 0 (a ≠ 0)?
这是一个多数人都知道答案的问题。从中学的数学课堂上,我们知道寻找二次方程的根方法无外乎因式分解,或者配方法,再或者跳去求解过程,直接代入求根公式中。
从某种意义上说,以上说的这些方法算不上不同方法,因为求根公式本就是通过配方法而推导得来的。
对求解任意二次方程的探索可追溯到4000多年前的古巴比伦时期。4000多年来,许多数学领域的知名人物都在这个现在看来十分简单的问题上留下了自己的记录。而二次方程的求根公式也成为了代数领域中的一个众所周知的标准公式。
2
最近,在一篇发表在arXiv的论文中,卡耐基梅隆大学的数学家Po-Shen Loh(罗博深)提出了一种求解二次方程的更简单的新方法。
罗博深认为通过配方法推导出的求根公式的计算有点“乱”,而且对一些初次学习代数的人来说,求根公式其实并不好记。再者,他认为传统的求根公式的推导过程其实颇有难度,因为“配方”这一概念本身就是智慧飞跃的结果,它并不容易。
在他新提出的方法中,他绕开了传统的配方过程,介绍了一种更为直观的求解方法,可以用更少的步骤找到二次方程的根。
3
那么这个更适用于代数初学者的求解过程是怎样的呢?
现在,让我们考虑一元二次方程:

求解的第一步与传统的方法很像,将多项式 x² Bx C 写作 (x - R)(x - S) ,如果

那么R 和 S就是x² Bx C=0的两个根。
将(x - R)(x - S) 展开,再合并同类项,得到:

也就是说两根之和为