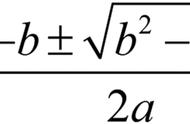4
作者在论文中举例了用新的方法求解二次方程:

首先要做的是在等式两边都乘以2,将x²的系数变为1,得到

根据上述方法我们知道,这个方程的两根之和等于2,两根之积等于4,也就是说1-z²=4,从而得出z=± i√3。
所以方程的两个根为

5
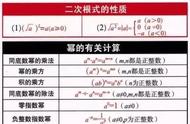
这种方法的优点在哪呢?罗博深认为,根据现在的代数课程设置,学生在了解二次方程之前,首先学会的是多项式相乘,比如他们懂得(a b)²=a² 2ab b²,以及 (a b)(a-b)=a²-b²。因此对于初学者来说,将两根之和的平均数作为参数,再在其基础上加减一个未知量,会是一种具有更直观的数学意义的技巧。因为与通过配方而推导出求根公式的过程相比,新的方法的动机更加直接。
罗博深的方法强化了每个二次方程都具有两个根的概念,简化了推导过程。通过引入两个根的平均值的概念,让运算的第一步变成搜寻的不是两个单独的、不同的值,而是一个相同的值。他认为,这种方法可以让学生不用去硬记某个公式来求解二次方程,而只要记住一些关于根的简单归纳,再最终找到方程的解。这将有助于学生理解二次方程是如何工作的,或许能帮助他们更好地适应数学。
参考链接:
https://arxiv.org/pdf/1910.06709.pdf