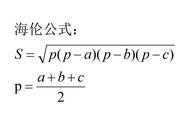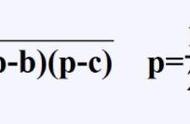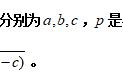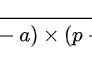本文为“第三届数学文化征文比赛
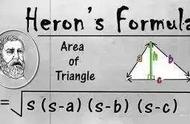
海伦公式
作者: 陆前进
作品编号:028
一、你从哪里来
早期的算术和几何在古代人们的生活中起了不小的作用,他们从实际生活中产生了计数以及度量方面的基本运算,在土地测量和简易工程方面获得了一定的几何知识。但他们的成就都是经验知识的结果,那时只要数学方面的知识能应付实际生活中的问题,人们就感到满足了。
对上古时代的人来说,只是由于生活需要的驱使,人们才去追求知识,为了知识本身而去追求知识的观念,一直要等到希腊人来进行。希腊人通过对自然现象的细致考察和理性思考,发展出一种概括、抽象、推理的能力,他们不仅在数学的各个部分作出了显著的、不朽的贡献,而且还为它们以后的发展奠定了永久的基础。
数学的抽象和严谨,是一种独特的看待世界的方式,这种方式来自于希腊古典时期,这个时期指的是大约从公元前600年持续到公元300年的这一段时间,涌现出像泰勒斯(公元前625年—前547年),毕达哥拉斯(公元前572年—前501年),欧几里得(公元前330年—前275年)和阿基米德(公元前287年—212年)等璀璨的名星。希腊人坚持演绎推理作为数学证明中唯一的方法是为数学作出的最重要的贡献,它使得数学从木匠的工具盒和测量学等实际背景中解放出来。从此以后,人们开始靠理性而不是凭感觉去判断什么是正确的,正是依靠这种判断,希腊人创造了我们今天所看到的这门学科,为人类文明、科技进步开辟了道路。
希腊人专注于自己的理念世界,在罗马强大的军事力量面前不堪一击,从公元前212年叙拉古城陷落于罗马的马塞卢斯之手阿基米德被*害到公元30年,罗马正式成为帝国,对西方世界行使着史无前例的统治。
阿基米德在数学景观上投入了长长的影子,其后的古代数学家虽然都有自己的建树,但却没有人能够比得上叙拉古城这位伟大的数学家。阿基米德之后的数学家有两位值得介绍,其中一位是阿波罗尼奥斯(公元前约262—190年),其代表作《圆锥曲线》被公认为是圆锥曲线问题的权威论述,当近二千年以后的开普勒作出他关于行星以椭圆形轨道围绕太阳运动的独创性理论时,圆锥曲线的重要性得到了证实,椭圆绝不仅是古希腊数学家手中好玩的珍品,它成为地球和地球上我们全体人类运行的轨道。《圆锥曲线》这部巨著与欧几里得的《几何原本》和阿基米德的著作并列成为古希腊数学的里程碑。
另一位就是阿波罗尼奥斯之后亚历山大的海伦(约公元前1世纪—公元1世纪之间)我们对他的生平知之甚少,现代人一般认为其活动时期为公元75年前后。海伦无疑受古希腊理性思想的影响在数学上有很深的造诣。随着希腊数学的衰落,他的兴趣倾向于实践方面。他的很多著作都涉及了实用科学,如机械学、工程学和测量学,在某种意义上也反映了希腊人与罗马人兴趣的截然不同。海伦在其《经纬仪》一书中介绍了挖掘穿山隧道及计算泉水流量的方法,在另一部著作中,他回答了一些日常的生活问题,如“为什么用膝盖在一根木棍的中间用力顶,木棍会容易折断?”或者“为什么人们用钳子而不用手拔牙?”之类的问题。当然,海伦的代表作是《度量》一书,主要讨论了各种几何图形的面积和体积的计算,其中就包括我们重点要介绍的后来以他的名字命名的关于三角形面积的公式,出自《度量》一书中的命题Ⅰ8,海伦对这一命题的证明是古典几何抽象推理的典范。
二、教我如何不想她
三角形面积的标准公式十分简单——,应用广泛,但是,如果用这个公式去求如图1中的三角形面积还要费些周折,因为我们还不知道三角形的高。

图1
三角形具有稳定性,已知一个三角形的三条边,其面积一定是确定的,这也可以直接从全等三角形“SSS”判定定理推导出来,例如,任何边长等于4、13、15的其他三角形一定与图1中的三角形全等,因此其面积也完全相等。
如何确定这一面积值呢?现代的我们拥有三角学的知识和代数变形能力,可以毫无困难的求出这个值。但是,最简便的方法仍(像两千年前一样)是应用海伦公式,其公式用现代符号表示就是:如果k是边长等于a、b、c的三角形的面积,那么
在应用海伦公式时,我们只要知道三角形的三条边,直接计算就行了,而无须求出三角形的高。
这是一个非常特殊的公式,公式中出现的半周长似乎非常奇怪,而4个数的乘积的平方根也令我们大部分人厌烦,这个代数运算令人头痛,然而,作为一个伟大的定理,引起我们注意的不仅有它的奇特,还有海伦为此所作的证明。
海伦的证明只用了一些简单的平面几何概念,也就是说,我们初中生就能完全弄懂,但是,海伦向我们展示了他精湛的几何技巧,他将一些初等几何的知识组合成一个非常丰富而漂亮的证明,既曲折,又非常巧妙,堪称数学中一个令人叹为观止的结论。
海伦的证明需要用到一些基本命题,这些命题对我们来说都不陌生:
命题1:三角形的角平分线交于一点,这个交点是三角形内切圆的圆心,简称内心。
命题2:从直角三角形的顶点作斜边的垂线,则垂线两边的三角形分别与原直角三角形相似,并互相相似。
命题3:在直角三角形中,斜边的中点与三个角的顶点距离相等。
命题4:已知ABCD是一个四边形,连接对角线AC与BD,如果∠BAC=∠BDC=90°,那么A、B、C、D四点共圆。
命题5:圆内接四边形的对角和等于两个直角。
海伦将这些命题作为“元素”,连同他那娴熟的几何技巧,带给我们一个关于三角形面积的证明。
定理:已知一个三角形,其边分别为a、b、c,记面积为k,那么,其中,是三角形的半周长。
设任意三角形,为了使海伦的论证清晰易懂,我们将证明分成三大部分。
第一部分:把面积k表示出来
海伦的第一步就出人意料,因为他首先作了一个三角形的内切圆,用三角形的内心作为确定其面积的关键因素,而圆的性质与三角形这种直线形的面积没有直观的联系。
如图2,作的内切圆,我们显然有面积

图2
海伦在三角形的面积k与其半周长s之间建立了联系,这说明方向走对了,当然,后面还有许多事情要做。
第二部分:把公式表达式中的线段表示出来

图3
如图3,延长BA至G,使AG=CE则有
因此 s-c=AG
s-b=BG-AC
=(BD AD AG)—(AF CF)=BD
同理 s-a=AD
这样,半周长s与s-a,s-b和 s-c三个量都等于图中的线段。这是富有启发性的结论,因为这些量都是我们所求证公式的组成部分,剩下的工作就是要把这些“零件”组合成一个完整的证明。
第三部分:证明的核心:找出有关量的关系