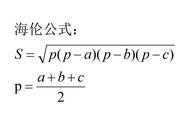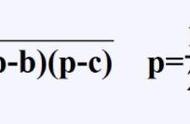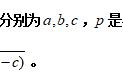海伦公式
01
本节所需要的一些基础知识:
①在直角三角形中,我们有射影定理(如图一):

CD^2=AD*DB, AC^2=AD*AB, BC^2=BD*BA
②在一般三角形中,我们有余弦定理:
在△ABC中,∠A、∠B和∠C的对边分别为a、b、c,则
a^2=b^2 c^2-2bccosA,b^2=c^2 a^2-2cacosB,c^2=a^2 b^2-2abcosC。
③在一般三角形中:
AD=ACcosA,BD=BCcosB;三角形的面积S=1/2ab·sinC=1/2bc·sinA=1/2ca·sinB.
④已知两个非零向量a、b,那么|a||b|cosθ(θ是a与b的夹角)叫做a与b的数量积或内积。记作a·b。两个向量的数量积等于它们对应坐标的乘积的和。即:若a=(x1,y1),b=(x2,y2),则a·b=x1·x2 y1·y2
如在图二中,
AB·AC=|AB|·|AC|cosA=|AB|·|AD|;BA·BC=|BA|·|BC|·cosB=|BC|·|BD|
但是在图三中,
AB·AC=|AB|·|AC|cosA=|AB|·|AD|;BA·BC=|BA|·|BC|·cosB=—|BC|·|BD|
02
海伦公式:假设在平面内,有一个三角形,边长分别为a、b、c,三角形的面积S可由以下公式求得:S=√[p(p-a)(p-b)(p-c)] 公式里的p为半周长:p=(a b c)/2
证明一:(利用勾股定理)
如图二,已知△ABC的三边长分别为a,b,c,CD为AB边上的高,记hc=CD,q1=AD,q=bd.由勾股定理得