二叉树和红黑树,二叉树和树的关系

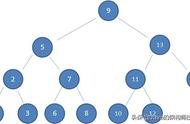
//旋转是红黑树的基础

那6个方向呢？

第一个是指向x的指针

第二个是指向Y的指针

第三个是x指向y的指针

第四个是y指向x的指针

第五个是y指向b的指针

第六个是x指向b的指针

//旋转是红黑树的基础 //为了判断叶子节点隐藏的都是黑色，那需要把整个红黑树都传进来 //以当前节点为轴心，这个当前节点是可以找到 //这个是左旋的函数 void rbtree_left_rotate(rbtree *T,rbtree_node *x) { //y等于x的右子树 rbtree_node *y = x->right; //1方向.现在x的右子树指向原来y的左子树 x->right = y->left; //如果y的左子树不是影藏节点 if(y->left != T->nil) { //2方向.原来y的左子树的父节点指向x y->left->parrent = x; } //这里旋转的时候，x是根节点,旋转完成后，y变为根节点 //3方向.现在y的parrent指向原来x的parrent y->parrent = x->parrent; //4方向.如果x的父节点是叶子节点，是空，代表x是root节点。 if(x->parrent == T->nil) { //那根节点指向y T->root = y; }else if(x == x->parrent->left) { //如果x是父节点的左子树,那么就把原来x父节点的左子树，指向y x->parrent->left = y; }else { //这种情况就把原来x父节点的右子树，指向y x->parrent->right = y; } //5方向.现在y的左子树指向了x y->left = x; //6方向.现在x的父节点指向了y x->parrent = y; } //x--y:需要换 //y-->x:需要换 //left-->right:需要换 //right-->left:需要换 void rbtree_right_rotate(rbtree *T,rbtree_node *y) { //y等于x的右子树 rbtree_node *x = y->left; //1方向.现在x的右子树指向原来y的左子树 y->left = x->right; //如果y的左子树不是影藏节点 if(x->right != T->nil) { //2方向.原来y的左子树的父节点指向x x->right->parrent = y; } //这里旋转的时候，x是根节点,旋转完成后，y变为根节点 //3方向.现在y的parrent指向原来x的parrent x->parrent = y->parrent; //4方向.如果x的父节点是叶子节点，是空，代表x是root节点。 if(y->parrent == T->nil) { //那根节点指向y T->root = x; }else if(y == y->parrent->right) { //如果x是父节点的左子树,那么就把原来x父节点的左子树，指向y y->parrent->right= x; }else { //这种情况就把原来x父节点的右子树，指向y y->parrent->left= x; } //5方向.现在y的左子树指向了x x->right= y; //6方向.现在x的父节点指向了y y->parrent = x; }

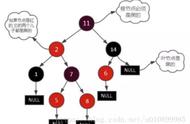
旋转后的解释就是，原来指向x的，现在指向了y。原来x指向左子树的，现在指向了x。x指向了Y的左子树。其它就是把parrent节点指向。

左旋不是原来的左右关系发生变化。不管是左右旋，红黑树的颜色都不会发生变化，旋转前需要判断颜色变化。旋转是为了寻求平衡。寻求平衡的目的是追求黑高的平衡，当黑高的高度不一致时，通过黑高来达到左右子树一致。

右旋，就是把原来的x换成y，y换成x。

//红黑树的插入与二叉树的插入是一样的性质，红黑树的插入也是插到最底下的叶子节点。

插入不会引起左右旋和其它改变。插入完成之后，会引起一个调整。

红黑树插入新节点之前，这个树已经是红黑树了。

插入节点

新插入的节点最好是红色，因为不影响黑高。如果新插入节点的父节点是红色，那么就需要调整二叉树，为什么？因为红色节点的子节点必须是黑色，这样也会影响黑高。

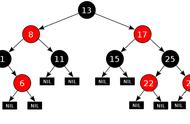
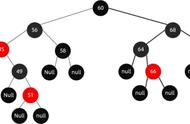
当前节点是红色，z的父节点是红色，z的祖父节点肯定是黑色的。叔父节点是可能是红色，可能是黑色

这里就存在3种情况：

第一种情况是插入的必须是红色节点(这也是确定的)，叔父节点是红色的,这个条件是确定的。

第二种情况是插入的必须是红色节点(这也是确定的)，叔父节点是黑色的。这个时候需要对祖父节点进行左旋。

第三种情况是插入一个900

//父节点为红色，就需要调整红黑树，否则会影响黑高 void rbtree_insert_fixup(rbtree * T,rbtree_node * z) { while(z->parrent->color == RED) { //如果父节点是祖父节点的左子树 if(z->parrent == z->parrent->parrent->left) { //获取叔父节点 rbtree_node *y = z->parrent->parrent->right; //如果叔父节点是红色 //这里有2种情况 if(y->color == RED) { //把父节点颜色变为黑色 z->parrent->color = BLACK; //当前节点也变为黑色 y->color = BLACK; //祖父节点变为红色 z->parrent->parrent->color = RED; //再以祖父节点为旋转即可调整黑高 z = z->parrent->parrent; }else { //如果叔父节点是黑色,这个时候就需要旋转 if(z == z->parrent->right) { //这个时候,父节点的右子树节点个数多，以父节点进行左旋 z = z->parrent; rbtree_left_rotate(T,z); } //定色 z->parrent->color = BLACK; z->parrent->parrent->color = RED; //再进行右旋 rbtree_right_rotate(T, z->parrent->parrent); } }else { //如果父节点是祖父节点的右子树 rbtree_node *y = z->parrent->parrent->left; if(y->color == RED) { //改变作色 z->parrent->color = BLACK; y->color = BLACK; z->parrent->parrent->color = RED; //轴心点 z = z->parrent->parrent; }else { if(z == z->parrent->left) { z = z->parrent; //右旋 rbtree_right_rotate(T,z); } //旋转第二次 z->parrent->color = BLACK; z->parrent->parrent->color = RED; //左旋 rbtree_left_rotate(T,z->parrent->parrent); } } } T->root->color = BLACK; } void rbtree_insert(rbtree *T,rbtree_node *z) { //y是叶子节点 rbtree_node *y = T->nil; //x是根节点 rbtree_node *x = T->root; while(x != T->nil) { //只要x不是叶子节点 y = x; 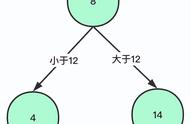if(z->key < x->key) { //如果要插入的值小于当前节点的值，那就往当前节点的左子树走 x = x->left; }else if(z->key > x->key) { //如果要插入的值小于当前节点的值，那就往当前节点的右子树走 x = x->right; }else{ //这表示要插入的节点已经存在了 return; } } //指向节点的末端,把z节点插入进来 z->parrent = y; if(y == T->nil) { //如果y的叶子节点为空 T->root = z; }else if(z->key < y->key) { y->left = z; }else { y->right = z; } //插入节点的左右子树指向空 z->left= T->nil; z->right = T->nil; //插入节点的颜色最好是红色，黑色会影响黑高 z->color = RED; //别忘了插入 rbtree_insert_fixup(T,z); }

红黑树和平衡二叉树区别？

平衡二叉树需要记录树的高度，是一个强平衡二叉树，当左右子树的高度大于1时，这个时候就需要调整。所以平衡二叉树旋转的次数，要比红黑树多。

为什么叔父节点是红色的时候，不需要旋转？

这个时候的黑高是一致的，只需要去改变颜色就行了。