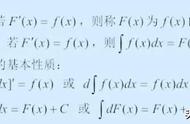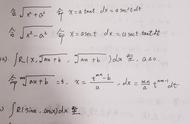数学上的一题三解是学习数学知识的一种很好的方法。通过一道题的多种解法比较,可以同时掌握多个几知识,更可以把这些知识点构成一个系统,融入自己的知识体系中,从而内化为自己的知识、能力。

下面是对一道不定积分进行三种不同的解法。解法一是第一换元积分法与分部积分法的结果,是教材提供的解法,最为烦琐。解法二剑走偏锋,只需用到分部积分法,相对更加简便,但是一般人容易忽略,想不到。方法三是直接运用老黄自己推出来的公式,最为直接,只要有公式的存在,几乎完全不用动脑和相关知识的支撑,就可以直接完成。我们来看看这个不定积分吧:
求∫x^3*lnxdx.
这是正整数幂函数与自然对数函数的积的不定积分。一般有自然对数函数出现的不定积分,多用第一换元积分法,就是记t=lnx,从而把自然对数函数化掉,并且有x=e^t,利用e^t的导数是它本身,能使得解题过程比较简便。
解1:令t=lnx, 则x=e^t, dx=de^t=e^tdt.
原积分=∫te^(4t)dt=1/4∫td(e^4t)=1/4*te^(4t)-1/4*∫e^(4t)dt
=1/4*te^(4t)-1/16*∫e^(4t)d(4t)=1/4*te^(4t)-1/16*e^(4t)
=1/4*x^4*lnx-1/16*x^4 C.

不过其实解法1并不简便。我们一般利用e^t的导数是它本身进行凑微分,是看重它凑微分之后不会升幂。而用幂函数凑微分之后,是会升幂的。所以一般人没有想到,这道题直接用幂函数凑微分,会更加简便。
解2:原积分=1/4*∫lnxd(x^4)=1/4*x^4*lnx-1/4*∫x^4d(lnx)
=1/4*x^4*lnx-1/4*∫x^3dx=1/4*x^4*lnx-1/16*x^4 C.

怎么样?是不是简便得多啊?不过它还不是最简便的。老黄之前推导过一个实数幂与自然对数函数的正整数幂的积的不定积分公式如下:
∫x^a*(lnx)^ndx=∑(i=0->n)(-1)^i*n!)/((n-i)!*(a 1)^(i 1))*x^(a 1)*(lnx)^(n-i) C.
直接套用这个公式更加快捷简便,这里的参数a=3, n=1.
解3:原积分=∑(i=0->1)(-1)^i/((1-i)!*4^(i 1))*x^4*(lnx)^(1-i) C=1/4*x^4*lnx-1/16*x^4 C.

实际上,求不定积分,基本上都是公式的运用。我们只是把复杂的不定积分转化成简单的不定积分公式来解而已。所以,只要有了对应的不定积分公式,再复杂的不定积分,也都是可以迎刃而解的。
,