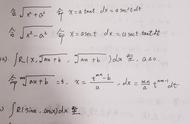今天我们来学一下不定积分的性质问题。
首先我们来看一下什么叫不定积分,既定义是什么。
定义:如果在区间A上,可导函数F(x)的导函数为f(x),既:对任意 X 属于A,都有如下形式:

我们再来看一下原函数存在定理:如果函数f(x)在区间A上连续,那么在区间A上存在可导函数F(x)。
这句话的意思就是说,连续函数一定有原函数。
接下来我们来看一下不定积分的定义:在区间A上,函数f(x)的带有任意常数项的原函数称为f(x)或f(x)dx在区间A上的不定积分,如下表述:

了解完不定积分的定义,我们接着往下看,不定积分的性质:

不定积分主要有两个性质,第一个性质称为不定积分的加法性质,就是说同时对两个函数的和求积分,可以分开求两个函数的积分,第二个称为不定积分的数乘性质,就是说当求一个数和一个函数同时求积分时,可以将这个常数提出来放到积分外面,直接求函数的积分即可。
我们来看一下这两个性质具体怎么运用

上面求解的两个题目包含了两个性质的运用,可以好好看一下,有不懂的可以直接留言回复。
,