①∵AB=AC,AD⊥BC,
∴AD平分∠BAC(或BD=CD);
②∵AB=AC,BD=DC,
∴AD⊥BC(或AD平分∠BAC);
③∵AB=AC,AD平分∠BAC,
∴BD=DC(或AD⊥BC).

【例4】 如图,在△ABC中,AB=AC,AD⊥BC,交BC于D,BD=5 cm,求底边BC的长.

4.等腰三角形的判定
(1)判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).

(3)理解:性质和判定应用的前提都是在同一三角形中,并且不经过三角形全等的证明,直接由等边得等角或由等角得等边,所以应用起来更简单、便捷.
破疑点 等腰三角形的判定方法的理解
教材中涉及等腰三角形的判定方法主要有两种:一是判定定理;二是定义.另外还有很多方法,如在同一个三角形中,三线中两线重合,也能说明是等腰三角形.但不常用,一般是通过推理得出角相等或边相等,再得出是等腰三角形.
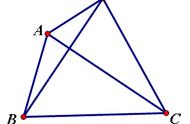
【例5】 如图,BE平分∠ABC,交AC于E,过E作DE∥BC,交AB于D.试证明△BDE是等腰三角形.