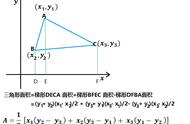
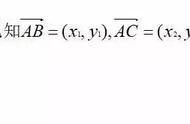求解直角三角形的面积-初中题
一个直角三角形ABC的斜边为AB, 其边长AC=15, 斜边的高线CH将斜边分成AH和HB两段, 其中HB=16, 求三角形ABC的面积。

解法:在两个直角三角形ACH和CBH中,有相等的三个角,所以两个三角形相似,或利用直角三角形的投影定理,可以得出:
AC·AC=AH·AB,
设AH=x,
可以列出方程:
15·15=x(x 16)
解这个方程得x=9,
在直角三角ACH中,AC=15, AH=9,利用勾股定理,可以看出这是一个3-4-5类型的直角三角形,所以可以得出CH=12,
而AB=AH HB=9 16=25,
所以三角形ABC的面积=AB·CH/2=25·12/2=150
,