1、公式求和法
等差数列前n项和:=,或者=;
等比数列前n项和:=n(q=1),或者=(q1);
2、分组求和法
例如:数列 1,3,5,7……求前n项和
解:(1)分组
=(1 3 5 7 ……) ( ……)
(2)计算:等差数列求和 等比数列求和
=[]
=
3、并项求和法(适用于数列通项公式=f(n)的形式)
例如:=,求前100项和
解:=- - -……- -
=(- ) (- )-…… (- ) (- )
使用平方差公式得到
=1 2 3 4 …… 97 98 99 100=5050
4、错位相减求和法(适用于数列,其中是等差数列,是等比数列的形式)
例如:数列通项公式为=(n 1),求前n项和
解:=2 3 …… n (n 1) ①式
2= 2 3 …… n (n 1) ②式
①式-②式(错位相减)
-=2 (1 1 …… 1)-(n 1)
-=4 -(n 1)=-n
=n
5、裂项相消求和法
适用于通项公式为以下情况的数列求和:
(1)=;
(2)=();
(3)=(分母有理化);
例如:数列通项公式,求前n项和
解:=1- - …… =1-=
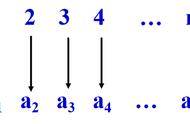
6、倒序相加求和法
例如:等差数列=公式的推导过程
解:= …… ①式
= …… ②式
①式 ②式得到
2=n( ),所以=。