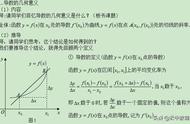
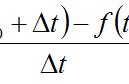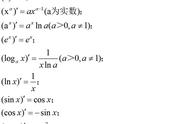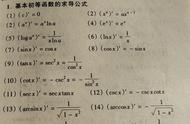导数的几何意义出题规律
导数的几何意义是高考命题的重点,主要有以下命题角度:
(1)求已知函数图象上某点处的切线方程;
(2)已知切线方程求函数解析式中的参数;
(3)利用导数的几何意义求解最值.
题型以选择题和填空题为主,分值为5分,属于中低档题,有时也出现在解答题的第一问中.

例1:[2018全国卷Ⅱ,13,5分][理]曲线y=2ln(x 1)在点(0,0)处的切线方程为__________.
思路分析:先求导数,再根据导数几何意义得切线斜率,最后根据点斜式求切线方程.
解析:∵y′=2/(x 1),∴k=2,∴y=2x.
答案:y=2x
例2: [2018全国卷Ⅲ,14,5分][理]14.曲线y=(ax 1)e^x在点(0,1)处的切线的斜率为-2,则a=________.

所以a=-3.
答案:-3
总结:求曲线的切线要注意“过点P的切线”与“在点P处的切线”的差异,过点P的切线中,点P不一定是切点,点P也不一定在已知曲线上,而在点P处的切线,必以点P为切点.