圆环

弯角
但是我们遇到的往往不仅仅是这几类图形,而是由形组合、拼凑成的不规则的组合图形,它们的面积不能直接用这些公式计算,解题的整体思想是把不规则的图形转化为规则图形,用到的方法有代数法、和差法、转化法、割补拼接法、容斥原理等等。在本专题中,我们将重点介绍这些求面积的几种常见的特殊方法!
二、常见解题方法1、周长
例题一、如图所示,200米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。已知每条跑道宽1.22米,那么外道的起点在内道起点前面多少米?(精确到0.01米)

例题一
解析:
半径越大,周长越长,所以外道的弯道比内道的弯道长,要保证内、外道的人跑的距离相等,外道的起点就要向前移,移的距离等于外道弯道与内道弯道的长度差。虽然弯道的各个半径都不知道,但是两条弯道的中心线的半径之差等于一条跑道之宽。

例题一
2、面积
(1)代数法
将图形按形状、大小分类,并设合适的未知数,通过建立方程或方程组来解出阴影部分面积的方法,或者通过未知数建立等量关系,不一定要求出未知数!
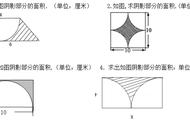
例题二、如图正方形的边长为a,分别以两个对角顶点为圆心、以a为半径画弧,求图中阴影部分的面积。