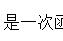刘维尔
原来在1844年,法国数学家刘维尔构造出这个数(这种构造性的做法是数学证明中一个常用的方法),潜心研究,终于发现,这个数不可能满足任何整系数代数方程,由此证明了它不是一个代数数,而是一个超越数。因此,第一个超越数也称“刘维尔数”。
在1873 年,法国数学家夏尔·埃尔米特也证明出自然底数 e 是一个超越数。

夏尔·埃尔米特
1882 年,德国数学家林德曼证明了圆周率 π 是一个超越数。(从此,π的神秘面纱也慢慢揭开。)
在研究超越数的过程中,莱昂哈德·欧拉曾提出猜想:若a是不等于0和1的代数数,b是无理代数数,则a^b是超越数。
这个猜想已被证明,于是可以断定e、π是超越数。
像无理数的发现一样,超越数的证明,也给数学带来了一场大变革,它解决了几千年来数学上的难题——尺规作图三大问题(即倍立方问题、三等分任意角问题和化圆为方问题)。
倍立方问题:有一个立方体,如何生成该立方体体积两倍的新立方体。
三等分任意角问题:在只用圆规及一把没有刻度的直尺将一个给定角三等分。
化圆为方问题
:是古希腊尺规作图问题之一,即:求一正方形,其面积等于一给定圆的面积。
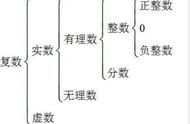
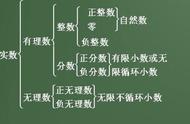
然而,人们对超越数的了解还是太少。至今数学家们仍然不知道,π e、π - e、π·e、π/e 这些数是否是超越数。。。
尽管如此,人们还是普遍相信它们都是超越数,毕竟它们不大可能恰好满足一个各项系数都是整数的多项式方程。

小天:嗯,有道理。。。不过,“超越数”这个词有点“辣眼睛”啊。

超模君:你以为讲到超越数就完了?还有更“辣眼睛”的数呢。。。
事实上,π的小数部分展开看上去是毫无规律的,但毕竟还是有办法算出来的。
可以说,如果想知道 π 的小数点后第一亿位是多少,人们总能在有限的时间里算出结果来。