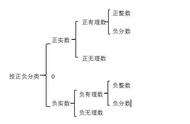
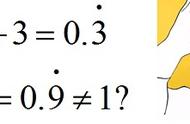数学的探索总是那么让人着迷!!!
就在1975年,数学家格里高里·蔡廷(算法信息论创始人)研究了一个很有趣的问题:任意指定一种编程语言中,随机输入一段代码,这段代码能成功运行并且会在有限时间里终止(不会无限运行下去)的概率是多大?
他把这个概率值命名为了“蔡廷常数”(Chaitin's constant)。
这听起来有点不可思议,但事实上确实如此——蔡廷常数是一个不可计算数(uncomputable number)。
也就是说,虽然蔡廷常数是一个确定的数字,但现已在理论上证明了,它是永远无法被求出来的。。。
小天背脊一凉:哈哈……不可计算数……不可计算……数……
超模君(根本停不下来):其实还有一个“更大的boss”。。。
虽然蔡廷常数是算不出来的,但是我们却知道蔡廷常数是什么,至少它有一个明确的定义。
然而,你仔细想想,会不会存在一种我们完全无法给它定义的一类数呢?

细思极恐,很显然,这类数是存在的。
至于原因,其实很简单:长度有限的文字段落是可以逐一枚举的(虽然有无穷多),而全体实数是不能枚举的,因此总存在一些不可能用语言描述出来的数。这种数就叫做不可定义数(undefinable number)。。。
此时的超模君根本停不下来。。。


听完这一切的小天一脸懵逼。。。
不过仔细想想:先分(zhuang)享(bi)给11岁的表妹。
,