第一章:集合与常用逻辑用语
第一节:集合
1、集合:集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体,这些对象称为该集合的元素。表示方法:①集合A={a,b,c,d}其中a,b,c,d是集合A的元素,即用a∈A,b∈A ,c∈A ,d∈A表示,f不是集合A的元素,则f∉A。集合A是集合B的子集,则A⊆B。②集合A={x|x>a}。
常见的集合:
整数集Z:{……,-3,-2,-1,0,1,2,3,……}
自然数集N(Nature):即非负整数,包括0:{0,1,2,3,……}
正整数集N*或N :{1,2,3,……}
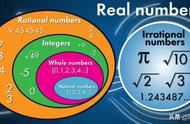
有理数集Q(有理数是两个数相比的结果(商)英文quotient):即整数和分数的集合
无理数集:小数点后面是无线不循环的数的集合,如:3.1415926
实数集R(real number):有理数和无理数的集合。
复数集C(complex number):实数和虚数的集合。
质数:质数又叫素数。在大于1的自然数中,除了1和它本身以外不不能整除其他自然数的数叫做质数。如:2,3,5,7,11。质数组成的集合为质数集。
合数:在大于1的自然数中,除了1和它本身以外能整除其他自然数的数叫做合数。如:4,6,8,9,12 。合数组成的集合为合数集。 * 1既不是质数也不是合数
2、子集:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。记作A⊆B或B⊇A,用韦恩(Venn)图表示如下:

(注意:x是集合A中的元素,用x∈A;集合X是集合A的子集,用X⊆A表示。)
真子集:如果集合A是集合B的子集,并且集合B不是集合A的子集,那么集合A叫做集合B的真子集。如果A包含于B,且A不等于B,就说集合A是集合B的真子集。
记作A⫋B(或B⫌A),用Venn图表示如下:

空集:指不含任何元素的集合。空集是任何集合的子集,是任何非空集合的真子集。空集不是无;它是内部没有元素的集合。可以将集合想象成一个装有元素的袋子,而空集的袋子是空的,但袋子本身确实是存在的。符号Ø
交集:设A,B是两个集合,由所有属于集合A且属于集合B的元素所组成的集合,叫做集合A与集合B的交集,记作A∩B

并集:给定两个集合A,B,把他们所有的元素合并在一起组成的集合,叫做集合A与集合B的并集,记作A∪B,读作A并B。

补集:一般指绝对补集,设U是一个集合,A是U的一个子集,由U中所有不属于A的元素组成的集合,叫做子集A在U中的绝对补集(简称补集)。记作写作∁UA,用Venn图表示如下:

非空集合子集的个数:假设非空集合A中含有n个元素,则有:

证明 : 集合A={1,2,3,4,5,……n}
集合A中每个子集都有出现和不出现两种可能。
1 出现或不出现2种可能
2 出现或不出现2种可能
3 出现或不出现2种可能
……
n 出现或不出现2种可能
根据乘法原理:共有2*2*2*2……*2=2n种不同的排列
3、集合的运算:
集合交换律:A∩B=B∩A ,A∪B=B∪A
集合结合律:(A∩B)∩C=A∩(B∩C) ,(A∪B)∪C=A∪(B∪C)
集合分配对偶律 :A∩(B∪C)=(A∩B)∪(A∩C),A∪(B∩C)=(A∪B)∩(A∪C)
集合对偶律:(A∪B)^C=A^C∩B^C ,(A∩B)^C=A^C∪B^C (A并B的余集等于A的余集交B的余集)
集合吸收律 :A∪(A∩B)=A ,A∩(A∪B)=A
集合求补律 :A∪∁uA=U ,A∩∁uA=Φ
集合的摩根律:∁u(A∩B)= ∁uA∪∁uB ,∁u(A∪B)= ∁uA∩∁uB
,