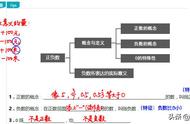
有理数是数学中非常重要的概念,以下是有理数知识大纲和相关的具体题目:
一、有理数的定义和分类
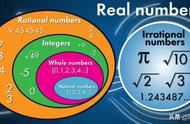
1. 有理数的定义:能表示为两个整数之比的数,包括整数、有限小数和无限循环小数。
2. 有理数的分类:
- 正有理数:大于 0 的有理数。
- 负有理数:小于 0 的有理数。
- 零:既不是正数也不是负数的有理数。
二、有理数的四则运算
1. 有理数的加法:同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
2. 有理数的减法:减去一个数等于加上这个数的相反数。
3. 有理数的乘法:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与 0 相乘都得 0。
4. 有理数的除法:除以一个不等于 0 的数,等于乘这个数的倒数;两数相除,同号得正,异号得负,并把绝对值相除;0 除以任何一个不等于 0 的数,都得 0。
三、有理数的大小比较
1. 正数大于 0,0 大于负数,正数大于负数。
2. 两个正数比较大小,绝对值大的数较大。
3. 两个负数比较大小,绝对值大的数反而小。
四、有理数的混合运算
有理数的混合运算顺序:先乘方,再乘除,最后加减;同级运算,从左到右进行;如果有括号,先算括号内的运算。
以下是一些具体的有理数题目:
1. 计算:3 (-5)。
解析:根据有理数的加法法则,同号两数相加,取相同的符号,并把绝对值相加。因此,3 (-5)=-2。
2. 计算:(-7)X(-3)。
解析:根据有理数的乘法法则,两数相乘,同号得正,异号得负,并把绝对值相乘。因此,(-7)X(-3)=21。
3. 比较大小:-5和-3。
解析:根据有理数的大小比较法则,两个负数比较大小,绝对值大的数反而小。因为| -5|=5,| -3|=3,5>3,所以-5
4. 计算:(-3)÷(-6)。
解析:根据有理数的除法法则,除以一个不等于 0 的数,等于乘这个数的倒数。因此,(-3)÷(-6)=½。
5. 计算:[(-2)^3-3^2]÷(-5)。
解析:根据有理数的混合运算顺序,先算乘方,再算乘除,最后加减。因此,
[(-2)^3-3^2]÷(-5)
=(-8-9)÷(-5)
=(-17)÷(-5)
=17/5
希望以上有理数知识大纲和具体题目能够帮助你更好地理解和掌握有理数的相关概念和运算。
如果你还有其他问题,请随时提问。
我是Q,欢迎关注[笑]