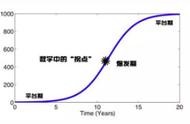
让我们先来看看当我们开车经过如上图这样的一段S形路时会发生什么。
为了让车辆沿着道路行驶,我们在A处首先微微向左转动方向盘,这时汽车就会向左转弯,然后保持在车道内行驶。凭借我们在驾校训练得到的经验,我们不用多加思索就知道当汽车经过B点时,我们应该平稳回正方向盘,之后紧接着继续向右微微转动方向盘,这时汽车便能向右转弯,然后继续平稳地沿着车道驶过S形道路的后半段。(A~B之间方向盘的方向其实没有变化,也就是说“没有拐”。)
注意到B点发生了什么吗?在B点处我们将方向盘回正了。B点之前的AB段,汽车的方向盘是处于左转状态;而B点之后的BC段,汽车的方向盘是右转的状态。在B点处,方向盘经历了从偏左到回正再到偏向右的变化。也就是说,B点处汽车经历了从左转状态到右转状态的状态转化。这也正是拐点这个词的来历,它表示了汽车行驶状态在该处会发生变化,也就是拐了一个弯。(也就是说B点方向盘方向发生了变化,“拐了”)

拐了、拐了
需要注意的是,不论是AB段还是BC段,汽车的位置始终都在向左偏移。换句话说,随着汽车不断前进,汽车的位置越来越靠左了。当我们最终完全驶过S型路段之后,汽车的行驶方向未发生变化,但位置和之前相比更靠左方了。
D点和E点虽然是看上去汽车方向发生最大的偏转的位置,但其实方向并没有切换。在驾驶过程中,方向盘方向发生变化,同时,车轮方向发生变化的点是B点。
车轮偏转方向切换的点,我们把定义成拐点的话。从行车轨迹上来说,也就是行车轨迹形状的凹凸改变的点。所以数学上更严谨的定义是:
拐点:使函数凹凸性改变的点。
那么首先我们来解释一下,什么是凹凸。一般来说,凹凸是个定性的词汇,并不是个定量的词汇。我们一眼看上去是凹的,就是凹的,一眼看上去是凸的。

但是有的函数往往不会是一直凹的,也不会是一直凸的。