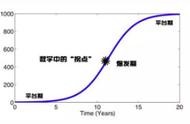
我们似乎很难找到那个由凸转凹的分界线,也很难找到由凹转凸的分界线。
我们想找到凹凸切换的准确的点。我们首先要把,凹凸给定量描述,而不能感性的定性描述。
我们知道,我们想看一个平面是凸的,还是凹的,就是用一个直尺放在这个平面上,如果两边接触,而中间没接触,则为凹的;相反,如果中间接触,而两边不接触,则为凸的。
数学上也是运用了一样的原理。
凹凸性的定义


一阶导数就是函数切线。一个函数的拐点可能是二阶导数为0的点,也有可能是二阶不可导点。至于为什么拐点处二阶导数为0,是这样的,一阶导数描述函数的变化,二阶导数描述一阶导数的变化,也就是斜率的变化情况,拐点处斜率大小由递增变为递减,或者由递减变为递增,这样自然二阶导数为0了。