判断顺推逆推口诀

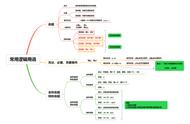
递推算法可以不断利用已有的信息推导（迭代）出新的信息，在日常应用中有如下两种递推算法。

① 顺推法：从已知条件出发，逐步推算出要解决问题的方法。例如斐波那契数列就可以通过顺推法不断递推算出新的数据。

② 逆推法：从已知的结果出发，用迭代表达式逐步推算出问题开始的条件，即顺推法的逆过程。

迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程，在解决问题时总是重复利用一种方法。与迭代法相对应的是直接法（或者称为一次解法），即一次性解决问题。迭代法又分为精确迭代和近似迭代。“二分法”和“牛顿迭代法”属于近似迭代法，功能都比较类似。

递归：一些复杂问题，分解后各子问题的解法与整体问题的解法具有相同结构（相同解法），同样的代码可以重复调用（自己调用自己）。函数递归调用时，通常有4个特点：

① 有一个递归终止条件，通常此条件的问题的解的规模为1，可直观求解；

② 递归函数的参数可以形成迭代关系，向递归递归终止条件收敛；

③ 以递归调用语句为基准，此语句前面的语句形成递归前进段，后面的语句形成递归回归段；如果函数参数有迭代关系，与简单的循环语句不同，递归函数的语句是分段执行的；

④ 递归语句分单递归，双递归及多递归等；单递归是指递归函数自己调用自己一次，双递归是调用两次，多递归是调用多次；双递归的调用形成一种二叉树的调用关系；

0 斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……

一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？

#include <stdio.h> int fib(int m) { int a = 1; int b = 1; m-=2; while(m--) // 顺推m-2次 { int c = a b; a=b; b=c; } return b; } int fibR(int m) // 递归，参数和返回值形成迭代关系 { return (m<3)?1:fibR(m-1) fibR(m-2); // 双递归 } int main() { printf("%d\n",fib(12)); // 144 printf("%d\n",fibR(12));// 144 setbuf(stdin,0); getchar(); return 0; }

简单推导：

1 猴子吃桃问题

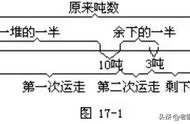
一只小猴子一天摘了许多桃子，第一天吃了一半，然后忍不住又吃了一个；第二天又吃了一半，再加上一个；后面每天都是这样吃。到第10天的时候，小猴子发现只有一个桃子了。问小猴子第一天共摘了多少个桃子。

#include <stdio.h> int phs(int days) // 使用两个变量迭代、逆推 { int tod = 1; int yst; for(int i=1;i<days;i ) { yst = 2*(tod 1); // yst/2-1 = tod tod = yst; } return tod; } int peaches(int days) // 使用单个变量迭代、逆推 { int tod = 1; for(int i=1;i<days;i ) { tod = 2*(tod 1); } return tod; } int pea(int d) // 递归，由参数和返回值做迭代 { if(d==1) return 1; else return (pea(--d) 1)*2; } int main(){ printf("%d\n",phs(10)); getchar(); }

2 自定义平方根函数

#include <stdio.h> double sqrt(double y) { double x0 = y/2; double x1,diff; const double epsilon = 1e-6; do{ x1 = (x0 y/x0)/2; x0=x1; // 两个变量逐步迭代 diff = y-x1*x1; }while(-epsilon>diff || diff>epsilon); return x1; } int main() { for(int i=1;i<=100;i ) printf("= %.4f\n",i,sqrt(i)); getchar(); return 0; }

3 最大公约数（greatest common divisor, highest common factor）

#include <stdio.h> int gcd(int a,int b) // a、b、a%b逐步迭代 { while(b!=0){ int r = a%b; a=b; b=r; } return a; } int gcdr(int a,int b) // 递归，由参数来做迭代 { if(b==0) return a; else return gcdr(b,a%b); } int gcd2(int a,int b) { int r; while(r = a%b) { a=b; b=r; } return b; } int main() { printf("%d\n",gcd2(36*71,36*82)); printf("%d\n",gcdr(36*70,36*80)); printf("%d\n",gcd2(36*81,36*72)); printf("%d\n",gcdr(36*80,36*70)); getchar(); return 0; } /* #include <iostream> using namespace std; */

4 字符串转整型

#include <stdio.h> long str2long(char s[]) { long res=0; int sign; while(*s==' ' || *s=='\t' || *s=='\n') s ; sign = (*s=='-'?-1:1); if(*s==' ' || *s=='-') s ; while(*s>='0' && *s<='9') { res = 10*res (*s -'0'); // 值以十进制方式逐步迭代 } return sign*res; } int main() { printf("%d\n",str2long(" 4321cdef")); getchar(); return 0; }

5 整型以二进制输出

void decToBin(int n) { if (n > 0) { decToBin(n / 2); // 递归，参数迭代 printf("%d ", n % 2); } }

-End-