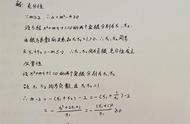①充分条件:一般地,用α、β分别表示两件事,如果α这件事成立,可以推出β这件事也成立,即α⇒β,那么α叫做β的充分条件。
注意:α是β的充分条件,则α⇒β,α成立能推出β成立,反之不一定成立。
原则:肯前必肯后,否后必否前。肯后必肯前不成立
结合实例解释为: x = 0 是 xy = 0 的充分条件:
肯前必肯后:即x=0成立,则xy=0必定成立。
否后必否前:即xy≠0成立,则x≠0必定成立。
肯后必肯前不成立:即xy = 0成立,则x = 0不一定成立。
②必要条件:如果β⇒α,那么α叫做β的必要条件。
注意:α是β的必要条件,则β⇒α,β成立能推出α成立,反之不一定成立。
原则:肯后必肯前,否前必否后。肯前必肯后不成立
结合实例解释为:如 xy = 0是 x = 0的必要条件:
肯后必肯前:即x = 0成立,则xy=0必定成立。
否前必否后:即xy≠0成立,则x≠0必定成立。
肯前必肯后不成立:即xy = 0成立,则 x = 0不一定成立。
③充分不必要条件,即α⇒β,而β⇏α;
④必要不充分条件,即α⇏β,而β⇒α;
⑤既充分又必要条件(充要条件),即α⇒β,又有β⇒α;
⑥既不充分也不必要条件,即α⇏β,又有β⇏α。
知识延伸:
①如果p,那么q(要是p,那么q):表示p是q的充分不必要条件。
例:如果小明参加比赛,那么小张也参加比赛;
则小明参加比赛,则小张一定参加比赛,
反之小张参加比赛,小明不一定参加比赛。
②只有p,才q:表示p是q必要不不充分条件。
例:只有小明参加比赛, 小张才参加比赛;
则小张参加比赛,则小明一定参加了比赛,
反之小明参加比赛,小张却不一定参加比赛。
习题:基础题:
一、选择题:
1.“a>b且c>d”是“a c>b d”的 ( )
A.必要不充分条件 B.充分不必要条件
C.既是充分条件又是必要条件 D.既不是充分条件也不是必要条件
2.“x^2-1>0”,是“x<-1”的()
A.充分不必要条件 B. 必要不充分条件
C.既是充分条件又是必要条件 D.既不是充分条件也不是必要条件
能力提升
一、选择题
1.a<0时方程ax^2 2x 1=0至少有一个负数根的()
A.充分不必要条件 B. 必要不充分条件
C.既是充分条件又是必要条件 D.既不是充分条件也不是必要条件
2.若A是B的充分条件,B是C的充分条件,B也是D的充分条件,C是D的必要条件,则D是A的()
A.充分不必要条件 B. 必要不充分条件
C.既是充分条件又是必要条件 D.既不是充分条件也不是必要条件
二、解答题:
题型一般为:根据充分必要性质,求参数范围。
1.已知p:x^2-4x-5≤0,q:|x-3|<a(a>0),若p是q的充分不必要条件,求a的取值范围。
2.已知p:-2≤x≤10,q:1-m≤x≤1 m(m>0),若﹁p是﹁q的必要而不充分条件,求m的取值范围。
3.已知p:|x-3|≤2,q:x^2-2mx m^2-1≤0,若﹁p是﹁q的充分而不必要条件,求m的取值范围。
4.已知全集U=R,非空集合

(1)当a=1时,求(∁uB)∩A;
(2)命题p:x∈A,命题q:x∈B,若q是p的必要条件,求实数a的取值范围。
习题参考答案基础题:
一、选择题:
1.“a>b且c>d”是“a c>b d”的 ( )
A.必要不充分条件 B.充分不必要条件
C.既是充分条件又是必要条件 D.既不是充分条件也不是必要条件

2.“x^2-1>0”,是“x<-1”的()
A.充分不必要条件 B. 必要不充分条件
C.既是充分条件又是必要条件 D.既不是充分条件也不是必要条件

能力提升
一、选择题
1.a<0时方程ax^2 2x 1=0至少有一个负数根的()
A.充分不必要条件 B. 必要不充分条件
C.既是充分条件又是必要条件 D.既不是充分条件也不是必要条件