搞懂这些经典圆系列,中考圆的题目就不成问题了。
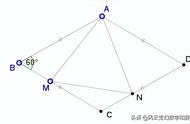
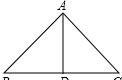
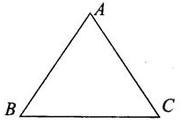
如图所示,圆O中的弦AB⊥CD于H,BE⊥AC于E,交CD于F;
(1)求证:HD=HF;
(2)若∠ABC=60°,求证:BD等于圆O的半径;

解题思路:辅助线如下图所示。

(1)根据等弧对等角,∠BDC=∠BAC;在Rt△ABE和Rt△BHF中,∠BAC ∠ABE=∠BFH ∠ABE=90°,所以∠BFH=∠BAC=∠BDC,即△BDF是等腰三角形,根据等腰三角形三线合一性质,BH也是中线,所以HD=HF;
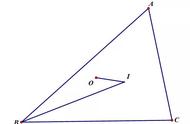
(2)如图,在Rt△BHC中,∠α=90°-∠ABC=90°-60°=30°;
(3)∠β=2∠α=60°(等弧对应的圆心角等于2倍的圆周角),所以△OBD为等边三角形(有一个角为60°的等腰三角形是等边三角形),所以BD等于半径。
小结:
这道题目要熟练掌握圆中相关角的换算,以及等弧对应的圆心角等于2倍的圆周角这个性质。
本题解答过程均为原创,如有错误之处,请大家不吝指正;如果有参考价值,建议关注收藏,谢谢。
,