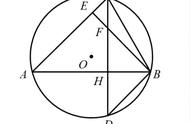
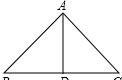
1、已知:如图,I、O为锐角△ABC内心、外心,且∠BIO=30° ,求∠BAC
思路分析:
不难猜出∠BAC=60° ,而且由第二篇知当∠BAC=60°时∠BIO=30°成立。下面关键是如何证明唯一性,基本思路是同一法。考虑到I、O为内外心,联想到鸡爪定理,延长CI交外接圆于E,则EB=EI,下面关键在于∠BIO=30°如何利用,需要说明∠BEI=60°,但是无法直接说明。经过尝试发现设B关于IO对称点为B’,则△B'BI为正三角形,B’B=B’I,从而B’与E重合,利用同一法,结论得证。

证明:如上图,做出外接圆O,延长CI交圆O于E,
由鸡爪定理得EB=EI。
设B关于IO对称点为B',
则由OB=OB’知B’在圆O上
且∠B'IO=∠BIO=30°,
故△B'BI为正三角形,故B'B=B'I,
又B'、E都在弧BAC上,且都在BI中垂线上,故B'、E重合,
则∠BAC=∠BEC=60°。
注:1)本题结论很容易猜出来,因为条件∠BIO=30°比较刁钻,很难利用,只能分别利用对称得到等边三角形,结合鸡爪定理说明B'、E重合才能最终得证。不过要彻底说清楚还是有点麻烦,需要作出外接圆综合鸡爪定理利用同一法才行。需要强调的是,用同一法容易出现“伪证”,我也是尝试了好几次都是伪证,经过认真修改才得到最终的正确结果。
2)本题采用暴力计算,采用正余弦定理或者心距公式也是可行的。
3)本题同一法还是比较有启发性的,不难想象,几乎所有的含有60°的三角形的判定都可以尝试利用类似思路解决。

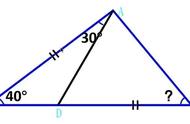
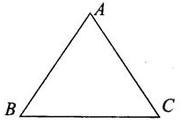
2、如图,在△ABC中,AP平分∠BAC且交BC于P,BQ平分∠ABC且交CA于Q.已知∠BAC=60°,且AB BP=AQ QB.问△ABC的各角的度数的可能值是多少?
思路分析:
最直接了当的思路是三角计算,应该不会太难。
如果希望用纯几何方法,
利用条件等式的自然思路是
在AB、AC延长线上截BF=BP,QB=QG。