今天和大家分享一道很有意思的初中数学几何题。这道题的慢点在于辅助线的构造,下面大家一起来看下这道题吧。
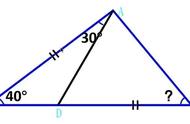
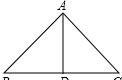
题目如下,在三角形ABC中,已知AB=DC,∠B=40度,∠BAD=60度,求∠C是多少度。

题干中的已知条件大多都在三角形ABD中,但是需要求的∠C却在另一个三角形中,我们需要将已知条件转化,和∠C产生联系。

看到题中有60度角,我们尝试来构造等边三角形,延长AD至点E,使AE=AB,因为∠BAD=60度,那么三角形ABE就是等边三角形。∠AEB=60度,在CD上取一点F,使EF=ED,三角形EDF为等腰三角形,∠EDF=80度,那么可得到∠DEF=20度,∠BEF=80度,从而得到BE=BF,因为CD=BF,可以推导出BD=CF,根据边角边,可以得到△BDE≌△CEF,进一步得到三角形BEC为等腰三角形。又因为AE=EC,∠AEC=80度,∠C=30度
,