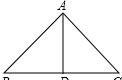
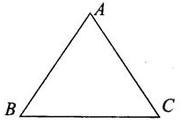
则AF=FG=GA且FP//BQ。
若G、C重合,则BQ=QC,
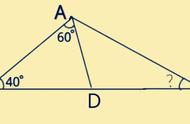
故∠ABC=80°=2∠ACB,显然满足条件。
所以可以先猜出答案,
估计只有这一种情况满足。
以下就是在G、C不重合的情况下,
则如何推出矛盾呢?
不难发现此时条件很难用。
经过长时间的尝试和探索,继续尝试消点。
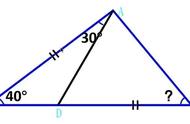
题目转化为正三角形AFG中,P在A的角平分线上,
B在AF上且BP=BF,
Q在AG上QB=QG,且BQ//FP,
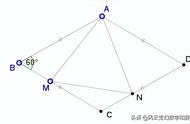
这样就能消去C点,得到下图

不难发现P确定后BQ随着确定,而若再有BQ//FP,
则P应该是确定的。
但未必是唯一的,而且应该也不是唯一的。
所以最好不用同一法,继续挖掘图形性质消点。
设FP交BG于L,则
∠BLF=∠QBG=∠AGB,
这样就能消去Q,得到下图,

∴∠BLF =∠AGB=∠AFK,
∠BKF=∠BLF-∠LFK=∠BFK-∠LFK =∠BFP=∠BPF,
则BFKP共圆,
故∠BFP=∠BKP>∠AGB=∠AFK>BFP
矛盾;
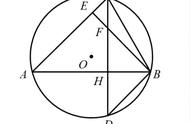
若L在FP延长线上,如下图

则依然如法炮制消去Q,有
∠BLF=∠QBG=∠AGB=∠AFK,
∴∠BKF=∠BFP=∠BPF,
则BFPK共圆,
则∠FBP=∠FKP=∠GKP=∠BFP=∠BPF,
故∠FBP=60°=∠BAC,
BC//AC,
矛盾。
综上,必有G、C重合,即∠ABC=80°。
注:1)本题初看似乎不难,但是要找到纯几何证明还是比较困难的,
这是当年IMO备选题几何中的最难的题目,参考答案的方法与上述
方法类似。国内林常教授也得到了一种纯几何证法。
此题难在如何充分利用条件得到共圆,
分类讨论要比较仔细。
2)上述本题的解题技巧还是很有启发性的,其实其推理过程和∠BAC=60°关系不大,即对一般的三角形也会有类似的结论。
3)当然本题用三角法应该是可以解决的,不过也需要一番三角计算。
,