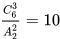如题,已知四边怎样求圆内接四边形对角线?请看题目:

图片
请看上图,怎样求对角线长度?图片来自链接:
https://m.toutiao.com/is/rpcH6AP/ - 求圆内接四边形的对角线,直接用全等三角形和勾股定理解题 - 今日头条
上面的链接提供了高中同学的解法以及作者的解法和数学老师的解法:
显然∠A ∠C=180°。高中学生用余弦定理可以快速做出。
BD²=3² 2²-12cos∠A
=4² 2²-16cos(180°-∠A),
13-12cos∠A=20 16cos∠A,
cos∠A=-1/4。
BD²=3² 2²-12cos∠A
=13 12×(1/4)=16,BD=4。
另外一条对角线可以用类似方法求出,也可以用托勒密定理来求。设两条对角线是e和f,那么托勒密定理说:
ac bd=ef
所以,另外一条对角线等于7/2.
求对角线的公式上面的链接没有给出求对角线的公式,本文介绍通用公式和相关证明。用公式可以轻松求出两条对角线的长度。
《数学奥林匹克中级读本(下)》(四川大学出版社出版,1991年10月第二版)一书中有这样一道例题(P75,例6):
如下图,设圆内接四边形 ABCD 的四边 AB = a , BC= b , CD = c , DA = d ,求对角线 AC 和 BD 的长
(要求用 a , b , c , d 来表示).

图片
书中在用余弦定理和圆内接四边形内对角之和为180°求出了两对角线之长后,有如下说明:“这例题用托勒密定理是不能求出圆内接四边形对角线的长。”然而我们说这说明是不正确的,用托勒密定理同样也能求出圆内接四边形的对角线长,现具体推理如下:
命题 已知圆内接四边形 ABCD 的四边 AB = a , BC= b , CD = c , DA = d ,求证:

求对角线的公式
图片
证明一