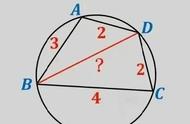
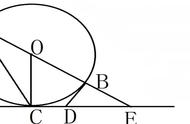
题目1:如图1,四边形ABCD内接于圆O,且AC⊥BD,垂足为E,F为AD的中点,连接FE并延长交BC于G。证明:FG⊥BC 。

解题思路:在Rt△AED中(图2),F为斜边AD中点,则FA=FE=FD,根据等腰三角形、对顶角、同弦对等角的性质将相等的角标于图中,易证α θ=90°,FG⊥BC成立。

此题为婆罗摩笈多定理的证明过程,即若圆内接四边形的对角线相互垂直,则四边形的一边中点与对角线交点的连线垂直于这条边的对边。反过来,若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将对边平分,证明方法类似,不再赘述。
题目2:如图1,已知四边形ABCD内接于圆O,对角线AC⊥BD,垂足为E,F为AB的中点。求证OF=1/2 CD。

解题思路(一):连接AO并延长交圆于G,则
∠ABG=90°,O、F分别为AG、AB的中点,
OF为Rt△ABG的中位线,OF=1/2 BG。
根据同弦对等角的性质,∠ADB=∠AGB=α。
在Rt△ABG和Rt△AED中,
∠BAG=∠DAE=θ(等角的余角相等)。
根据相等的圆周角所对的弦相等,BG=CD ,
OF=1/2 CD成立。