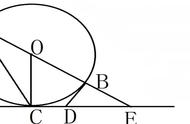
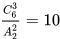解题思路(二):见图3。

解题思路(三):根据婆罗摩笈多定理,过点E作EG⊥AB,垂足为G(图4),延长GE交DC于M,则M为DC中点,MG∥OF。
连接OM,根据垂径定理,OM⊥DC。
连接FE并延长交DC于H,则FH⊥DC,OM∥FH,
故四边形OFEM为平行四边形,OF=ME。
在Rt△DEC中,M为斜边DC中点,则ME=1/2 CD,
故OF=1/2 CD成立。

解题思路(四):联想到“三角形任一顶点到垂心的距离等于外心到对边距离的两倍”这一结论,过点D作
DG⊥AB,垂足为G(图5),DG交AE于H,因AC⊥BD,
则H为△ABD的垂心,OF=1/2 DH。
易证△DHC为等腰△,DH=CD,
OF=1/2 CD。

解题思路(五):见图6。