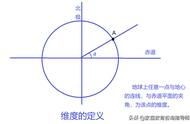
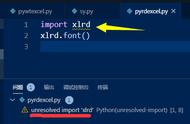
我们通过Java程序进行对赤道带足印位置的追踪。
1)依次增加 δ 值,并在其大于360度后减去360。
2)将数值保存在动态数组中,模拟卫星足印带在赤道上的覆盖点。
3)在数组中查找与该点相邻两点,即数值最接近的两个,将其与其相邻点的距离与临界值 dt 进行比对,如果小于临界值,则代表该两个足印之间没有区域未被足印区覆盖。为方便统计分析,我们将足印位置以角度 dt 储存,将距离转化为角度单位

当数组中所有点与其相邻两点距离均小于 dt 时,意味着赤道带将会被足印区完全覆盖,程序停止运行,并给出最终结果周期数n。
代入具体卫星运行周期T高度h,以及周期数n,便可得出最后问题所求总覆盖时间

《数学教学》编者注:选手没有说明临界值 dt 是如何确定的,dt 的精度决定了卫星运行的周期数n和全覆盖的时间t,因此这个解法无法说明是“最少时间”。
2.3 对问题(3)的解法讨论
一、台北中山女子高级中学队的解法
为了确定卫星的位置,假设卫星上装设了四个高度计,那么可以同时测量卫星与四个地面接收站的距离(见图7),我们将距离以及地面接收站的空间坐标替换成三元一次方程式,进而算出卫星在空间的坐标。

图7
假设卫星的空间坐标为 S(x,y,z),而四个地面观测站的坐标分别是A(a1,a2,a3)、B(b1,b2,b3)、C(c1,c2,c3)、D(d1,d2,d3),卫星测出与四个地面观测站的距离分别为h1、h2、h3、h4。则