聪明的古希腊人在两千年前就测出了地球的周长,他是如何做到的?
关于地球的形状,古希腊学者有好几种不同的观点:有人认为是平的,呈圆盘状或长方形;但也有很多人正确地认为是圆球体,因为他们判断,月食时在月亮上出现的圆弧形阴影正是地球的投影。时任亚历山大城图书馆馆长的著名数学家埃拉托色尼根据克莱门德(Cleomedes )在《论天体的圆周运动》中的描述,他通过比较两个已知南北距离的地点在正午时太阳高度来计算地球周长。
我们来看看埃拉托色尼根据克莱门德测量具体方法。已知西恩纳(Syene,今天的阿斯旺)地区,在夏至日那天正午时太阳直射井底,而且亚历山大港和西恩纳大致在同一经度上,又知道商队旅行时测量的两地之间的距离为5000古希腊里(一般认为1古希腊里约为158.5米),即两地相距约800公里。

阿斯旺和亚历山大港的位置
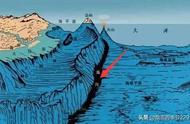
埃拉托色尼了解到,在每年的夏至日正午,太阳光直射到赛因(现为埃及的阿斯旺)中一口深井的井底;与此同时,在距离赛因正北约5000希腊里的亚历山大城,太阳光线与地面垂直线有2π/50弧度(7.2°)的夹角。假设太阳光线是平行的,则根据圆周长的计算公式,地球沿着通过南北两极的子午线周长为
周长= 5000×2π÷2π/50 = 250000希腊里。
按雅典的长度单位,1希腊里等于185米,由此得到地球的周长是46000多千米。按埃及长度单位,1希腊里等于157.5米,地球周长约39000多千米。
现在人们已经精确地测量到,地球的子午线周长是40008千米。由此可见,2000多年前埃拉托色尼的计算还是比较准确的。

古希腊数学家计算地球周长示意图
埃拉托色尼的另一个重要数学贡献是发明了筛选素数的有效方法--后人称之为"埃拉托色尼筛法"。
无独有偶,波塞多纽(Posidonius)同样参考了克莱门德(Cleomedes)在《论天体的圆周运动》中的描述,根据老人星(Canopus,青白色,亮度仅次于天狼星,中国南方可以看到它在近地平线处出现。)在天空中的位置计算了地球的周长。
根据资料显示,老人星(Canopus)从来没有出现在罗德岛(Rhodes)的地平线之上,而在亚历山大,他看见了它在地平线之上7.5°(而实际上两个地区纬度之间的子午线弧度是5°14')。

波塞多纽(Posidonius)测量地球周长的方法
由于波塞多纽(Posidonius)认为罗德岛在亚历山大港正北方距离为5000个体育场(stadia,古希腊长度单位,一个体育场大约等于现代英里的1/10)。