1、匀强电场中电势差与电场强度的关系

(1)UAB=Ed,d为A、B两点沿电场方向的距离。
(2)沿电场强度方向电势降落得最快。
(3)在同一直线上或相互平行的两条直线上两点间电势差与线段长度成正比。
2.匀强电场中的等势线
匀强电场中的等势线,等势面是一簇平行直线,平行平面。
连接两等势点的直线即为等势线。
3.带电粒子在匀强电场中的运动
电荷在其中受到恒定电场力作用(类似重力),带电粒子在其中只受电场力时做匀变速运动(类抛体运动)。带电粒子在匀强电场中受力是恒力,恒力作用下的运动有6种,都是匀变速运动,其中3种匀变速直线运动,3种匀变速曲线运动。
(1)直线运动:
a.类自由落体运动(初速度为零的匀加速直线运动)
b.类竖直下抛运动(初速度不为零的匀加速直线运动)
c.类竖直上抛运动(先匀减速
后反向加速)
(2)曲线运动:
a.类平抛运动
b.类斜上抛运动
c.类斜下抛运动
如果要考虑重力的话,把重力和电场力合并,恒力合并仍然是恒力,称为等效重力。
4.E=U/d在非匀强电场中的应用
(1)解释等差等势面的疏密与电场强度大小的关系:当电势差U一定时,电场强度E越大,则沿电场强度方向的距离d越小,即电场强度越大,等差等势面越密。
(2)定性判断非匀强电场电势差的大小关系:如距离相等的两点间的电势差,E越大,U越大;E越小,U越小。
例题:如图所示,

A、B、C、D、E、F为匀强电场中一个边长为10cm的正六边形的六个顶点,A、B、C三点电势分别为1V、2V、3V,正六边形所在平面与电场线平行.下列说法正确的是(ACD)
A.通过CD和AF的直线应为电场中的两条等势线
B.匀强电场的电场强度大小为10V/m
C.匀强电场的电场强度方向为由C指向A
D.将一个电子由E点移到D点,电子的电势能将减少1.6×10⁻¹⁹J
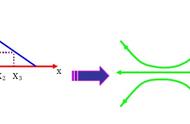
例题:空间存在着平行纸面的匀强电场,但电场的具体方向未知,现用仪器在纸面内沿互成60°角的0A、0B两个方向探测该静电场中各点电势,得到各点电势与到点距离的函数关系如图所示,

则下列关于该电场的电场强度E的说法中,正确的是()
A.E=400V/m,沿AO方向
B.E=200V/m,沿BO方向
C.E=200√3V/m垂直OB向下
D.E=200√3V/m,垂直OA斜向右下方
【解析】在匀强电场中,沿着任意一条直线(垂线除外),电势是均匀变化的。
利用等分法找到等势点。
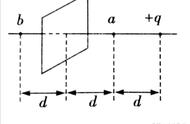
例题(湖南高考题)如图,

圆心为0的圆处于匀强电场中,电场方向与圆平面平行,ab和cd为该圆直径.将电荷量为q(q>0)的粒子从a点移动到b点,电场力做功为2W(W>0);若将该粒子从c点移动到d点,电场力做功为W.下列说法正确的是(AB)
A.该匀强电场的场强方向与ab平行
B.将该粒子从d点移动到b点,电场力做功为0.5W
C.a点电势低于c点电势
D.若只受电场力,从d点射入圆形电场区域的所有带电粒子都做曲线运动
【解析】
方法一:等分法找等势点

从d点延长R到f点,Wab=2W
则WOb=W,Wcd=W,则WOf=W,f和b点是等势点,fb是等势线,电场线沿着ab方向并且由高电势指向低电势。
方法二:把电场看作由Ex和Ey组成,利用合力的功等于各分力功的代数和。