反函数求导法则是微积分学中一个重要的法则,它的基本思想是通过对反函数的存在性进行证明,然后利用复合函数的求导法则来推导出反函数的导数。
这个法则在实际应用中有着广泛的应用,例如在自然科学、工程技术等领域中都有广泛的应用。
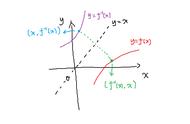
反函数的存在性定理是反函数求导法的基础。
这个定理指出,对于一个单值函数f(x),如果它在区间[a,b]上单调递增或递减,那么它的反函数f -1(x)在区间[f(a),f(b)]上存在,并且满足f(f -1(x))=x。但是,如果函数f(x)在[a,b]上不单调,则反函数f -1(x)可能不存在。
在对反函数进行求导时,我们可以利用复合函数的求导法则。
假设函数y=f(u),u=g(x)的反函数为x=g -1(y),那么复合函数的导数为dy/dx=(dy/du)*(du/dx)。
因此,我们可以根据反函数的存在性定理和复合函数的求导法则推导出反函数的导数。
具体来说,对于反函数y=f -1(x),我们可以令x=f(u),这样u就是中间变量。
由于f(u)和f -1(x)是单调的,它们的导数存在且为1/f'(u)和1/f'(x)。根据复合函数的求导法则,我们有(du/dx)=1/f'(u),因此反函数的导数为(dy/dx)=(du/dx)*(1/f'(u))=1/f'(x)。
值得注意的是,反函数求导法则不仅适用于简单的反函数,还可以应用于更复杂的函数形式。
例如,对于多元函数的反函数求导,我们可以通过微分法来求解。
多元函数的微分法是通过引入偏导数来求解的,偏导数是函数对某个自变量的导数。利用多元函数的微分法,我们可以求解多元函数的反函数的导数。
总之,反函数求导法则是微积分学中一个重要的法则,通过对反函数的存在性进行证明,并利用复合函数的求导法则来推导出反函数的导数。
这个法则在实际应用中有着广泛的应用,例如在自然科学、工程技术等领域中都有广泛的应用。同时,反函数求导法则还可以应用于更复杂的函数形式,例如多元函数的反函数求导。