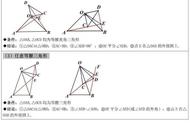
只是在这个模型中,条件有所变化,就是 a,b 都为正数了。
∴ y = 225 x 360²/x-360 ≥ 10440,当且仅当 225 x = 360²/x 时,等号成立。
即当 x=24m 时,修建围墙的总费用最小,最小总费用是 10440 元。
有意思的是,用这个基本不等式模型,可以解决类似的问题。比如,
1. 某游泳馆出售冬季学生游泳卡,每张卡 240 元.并规定不记名,每卡每次只限 1 人,每天只限 1 次.某班有 48 名学生,教师准备组织学生集体冬泳,除需要购买若干张游泳卡外,每次去游泳还要包一辆汽车,无论乘坐多少学生,每次的包车费为 40 元.要使每个学生游 8 次,每人最少交多少钱?
2. 某单位用木料制作如图所示的框架, 框架的下部是边长分别为 、 (单位: )的矩形.上部是等腰直角三角形. 要求框架围成的总面积为 . 问 、 分别为多少(精确到 0.001m) 时用料最省?

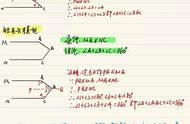
这或许就是数学模型方法在多题一解上的生动体现吧!更进一步地,运用此基本不等式模型,可以解决数学中一类不等式证明、求代数式的最值等问题。甚或还可以解决涉及其它知识点的问题。像,“若直线 x/a y/b = 1(a>0,b>0) 过点(1,1),则 a b 的最小值等于( )”就是联系解析几何的题目,曾经选为福建 2015 年的中考题呢!