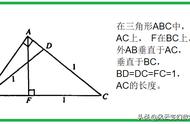
1求边长时会用到的定理主要有:三角形全等定理、中位线定理、等腰三角形和直角三角形特殊三角形;
2.相似三角形对应线段比等于相似比;
3.解几何题过程中一定要用数形结合思想,充分利用已知条件,挖掘隐藏条件,如何做辅助线等。
题1:

解答:
首先利用数形结合思想,利用已知条件BD=CD,即AD是中线,已知中线就要想到倍长中线法(解几何常用 的方法,指加倍延长中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则对应角对应边都对应相等)。
所以,我们把AD延长到E点,使AD=DE,则△BDE全等于△ADC,如下图:

在△ABE中,AB=10,AE=8,BE=6,所以∠E=90°,在△BDE中,勾股定理BD=2倍根号13,则BC=4倍根号13
题2:

解答:
首先正方形的边长会想到勾股定理,斜边可得5倍根号2,另外这是等腰三角形,则两边边角=45°,则设边长为x,则斜边为2倍根号2x,解得x=5/2cm,如下图:

题3:
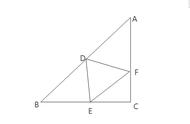
如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为

解答:
【分析】依据直角三角形斜边上中线的性质,即可得到EF的长,再根据梯形中位线定理,即可得到CG的长,进而得出DG的长.
【解答】解:∵E是边BC的中点,且∠BFC=90°,∴Rt△BCF中,EF=BC=4,∵EF∥AB,AB∥CG,E是边BC的中点,∴F是AG的中点,∴EF是梯形ABCG的中位线,∴CG=2EF﹣AB=3,又∵CD=AB=5,∴DG=5﹣3=2,
,